Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 4.10 - Ex. 160
Determine a força resultante equivalente do carregamento distribuído e sua localização, medida a partir do ponto . Avalie as integrais usando a regra de Simpson.
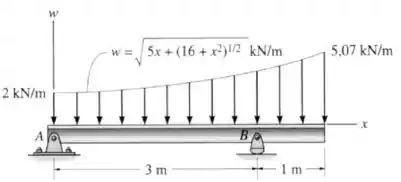
Passo 1
O primeiro passo aqui é calcular a intensidade da força total gerada pela distrubuição. Para isso temos que resolver a seguinte integral:
Mas o enunciado pediu para usarmos a regra de Simpson para calcular essa integral. Vamos nos lembrar da fórmula para isso.
A primeira coisa a fazer é dividir nosso intervalo (ou seja ) em um número par de subdivisões, cada uma com “comprimento” .
No nosso caso vamos usar subdivisões:
Então nossos pontos são e , por isso a fórmula para a integral vai ser a seguinte:
Passo 2
Agora vamos calcular o valor de para cada um desses valores:
E então podemos substituir tudo na fórmula principal, além de :
Essa é a intensidade da força gerada pela distribuição.
Passo 3
Agora, para determinar qual deve ser a localização da força, precisamos calcular o momento gerado pela distribuição, e então exigir que a nossa força produza o mesmo efeito.
A fórmula para o momento da distribuição também depende de uma integral que pode ser calculada com a regra de Simpson:
Onde é a distância de cada ponto da viga até o ponto .
Podemos aproveitar a fórmula que escrevemos antes, e usar o mesmo :
Também podemos aproveitar os valores que calculamos para , basta multiplicar pelo mais uma vez no final:
E então quando substituirmos na fórmula, encontramos o seguinte:
Passo 4
Beleza, agora é só calcular qual deve ser a distância até o ponto para que a nossa força produza esse mesmo momento :
Resposta
A força deve ter uma intensidade de e deve agir a uma distância de do ponto .