Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

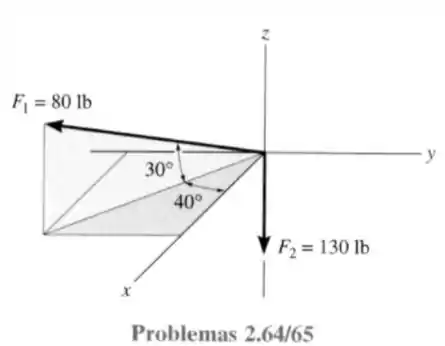
65- Especifique os ângulos diretores coordenados de F 1 e F 2 e expresse cada força como um vetor cartesiano.

Passo 1

Da questão passa temos:

F 1 = 53.07 i - 44.53 j + 80 sin ⁡ 30 k

F 2 = - 130 k

Onde 80 s i n 30 = 40

E as forças resultantes serão:

F 1 = 80   l b

F 2 = 130   l b

Passo 2

Com isso conseguimos resolver os ângulos diretores das forças. Começando pela F 1 :

α 1 = cos - 1 ⁡ F x 1 F 1 = cos - 1 ⁡ 53.07 80 = 48.44 °

β 1 = cos - 1 ⁡ F y 1 F 1 = cos - 1 ⁡ - 44.53 80 = 123.82 °

γ 1 = cos - 1 ⁡ F z 1 F 1 = cos - 1 ⁡ 80 sin ⁡ 30 80 = 60 °

Passo 3

Já para F 2 :

F 2 = 0 i + 0 j - 130 k

α 2 = cos - 1 ⁡ 0 130 = 90 °

β 2 = cos - 1 ⁡ 0 130 = 90 °

γ 2 = cos - 1 ⁡ - 135 135 = 180 °

Resposta

F 1 = 53.07 i - 44.53 j + 40 k

α 1 = 48.44 ° ; β 1 = 123.82 ° ;     γ 1 = 60 °

F 2 = - 130 k

α 2 = 90 ° ; β 2 = 90 ° ;     γ 2 = 180 °

Ver Outros Exercícios desse livro