Substitua o sistema de forças por uma força e um momento equivalentes no ponto .
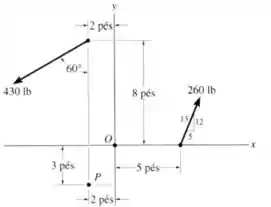
Passo 1
Para calcular o ângulo formado pela força de , vamos usar aquele triângulo representado ao lado do vetor no desenho:
E então podemos calcular o momento:
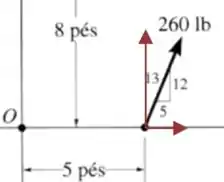
Agora fazemos o mesmo para a força de :
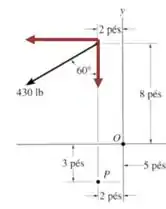
E então o momento total agindo sobre o sistema em relação ao ponto é:
Passo 2
Agora vamos calcular a força resultante. Para isso precisamos escrever cada uma delas em forma vetorial:
E então a resultante é:
Então o módulo da força é:
E o ângulo que esse vetor forma com o semi-eixo negativo é:
Resposta
As forças podem ser substituídas por um par formado por um binário e uma força de módulo a do semi-eixo negativo no ponto .