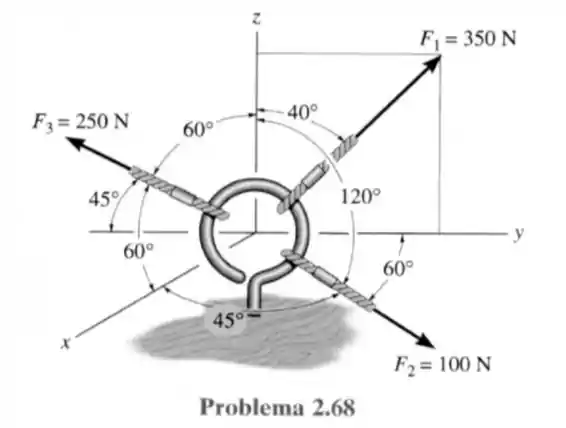
68- Os cabos presos ao olhal estão submetidos as três forças mostradas. Expresse cada força na forma vetorial cartesiana e determine a intensidade e os ângulos diretores coordenados da força resultante.
Passo 1
Cada força tem o seu ângulo diretor para cada eixo logo é só representar-lo vetorialmente.
Para força temos:
O que dá:
Agora para a força :
Agora para a força :
Passo 2
Somando vetorialmente todas as forças temos a força resultante que será igual a:
O que pode identificado como:
Com isso a intensidade da força será igual a:
Passo 3
Agora podemos encontrar os ângulos diretores da força resultante que serão calculados:
Continuando:
Para o úitimo ângulo: