Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.6 - Ex. 70

70- Determine a intensidade e os ângulos diretores coordenados da força resultante e esquematize esse vetor no sistema de coordenadas.

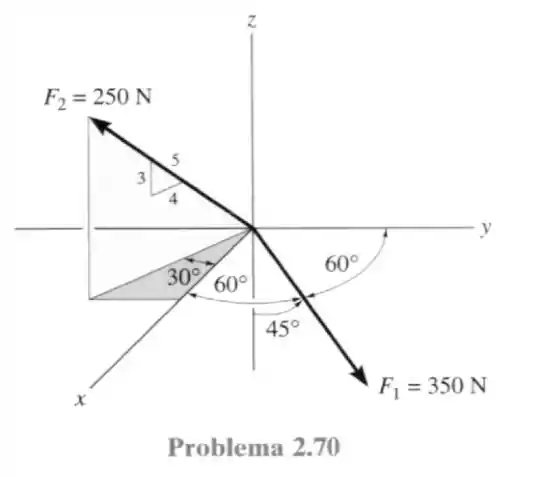
Passo 1

Os ângulos diretores da força F 1 foi dado na figura, logo a sua representação cartesiana será:

F 1 = ( 350 cos ⁡ 60 ) i + 350 cos ⁡ 60 j - 350 cos ⁡ 45 k

F 1 = 175 i + 175 j - 247.49 k   [ N ]

A força F 2 forma um ângulo θ com o plano x y cujo seno e cosseno vale:

sin ⁡ θ = 3 5 ;     cos ⁡ θ = 4 5

Dessa forma a representação cartesiana de F 2 valerá:

F 2 = 250 cos ⁡ θ cos ⁡ 30 i - 250 cos ⁡ θ sin ⁡ 30 j + 250 sin ⁡ θ k

O que dá:

F 2 = 173.21 i - 100 j + 150 k

Passo 2

Dessa forma a força resultante será:

F r = F 1 + F 2 = 175 + 173.21 i + 175 - 100 j + - 247.49 + 150 k

F r = 348.21 i + 75 j - 97.49 k   [ N ]

Isso nos dará uma magnitude de força igual a:

F r = 348.21 2 + 75 2 + - 97.49 2 = 369.3   N

Passo 3

Agora podemos encontrar os ângulos diretores da força fazendo:

α = cos - 1 ⁡ 348.21 369.3 = 19.46 °

β = cos - 1 ⁡ 75 369.3 = 78.28 °

γ = cos - 1 ⁡ - 97.49 369.3 = 105.31 °

Resposta

F r = 369.3   N

α = 19.46 ° ;     β = 78.28 ° ;     γ = 105.31 °

Representação do vetor F r no sistema de coordenadas.

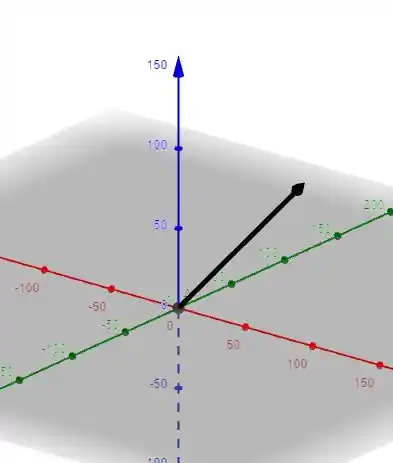
Onde a linha azul é o eixo z , a verde o eixo y e o vermelho o eixo x .

Ver Outros Exercícios desse livro