70- A lança é mantida em equilíbrio por uma junta esférica e um sistema de polias e cordas, como mostrado na figura. Determine os componentes da reação em e a tensão no cabo quando

Passo 1
A junta esférica apresenta resistência a força em todos os eixos, mas não apresenta resistência a torque, isso faz com que o sistema de força na lança seja a seguinte.

Passo 2
Fazendo a somatória das forças em temos:
Fazendo a somatória das forças em temos:
E fazendo a somatória das forças em temos:
Passo 3
E para achar essa força vamos fazer com que a somatória das forças em na barra percorrendo o eixo em seja de zero (ou seja calcular o momento em da barra sabendo que ela não encontra nenhuma resistência).
Isso nos dá uma força igual a:
E uma força igual a:
Passo 4
Agora vamos desenhar o sistema de polias para calcularmos a tração no cabo .

Como todo o eixo de polias encontra-se inclinado inclinado em relação ao eixo vamos calcular a tração na corda igual a pela somatória das forças no eixo paralela a todas as polias. Só que para isso precisamos calcular o ângulo formado pelo cabo e o ponto .
Para isso precisamos calcular o tamanho da distância que será a hipotenusa abaixo.
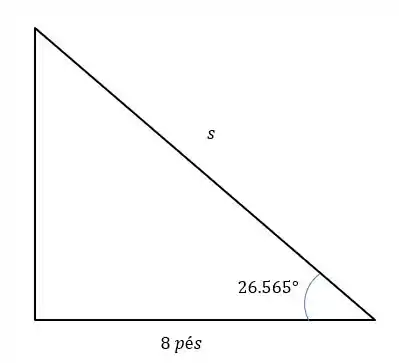
Logo:
Agora podemos calcular pelo triângulo retângulo a qual ela pertence da seguinte maneira:
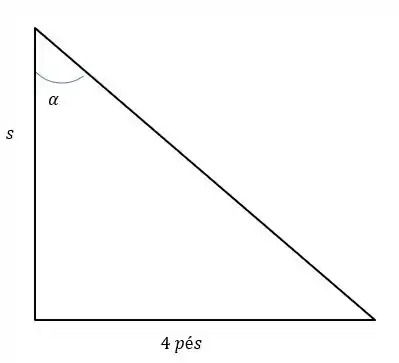
Passo 5
Agora basta fazer a somatória das forças em :