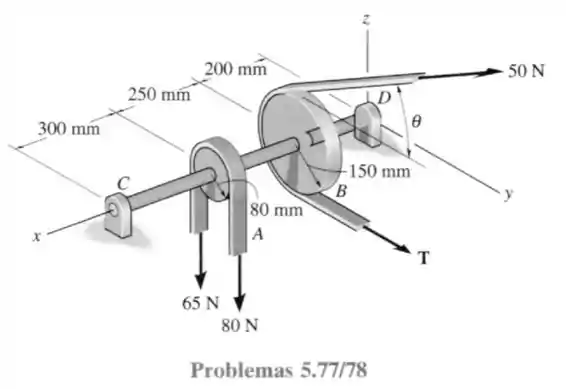
78- Determine agora a força horizontal na correia da polia e os componentes de reação no mancal simples em e no mancal de encosto em , quando . Os mancais estão adequadamente alinhados e exercem apenas forças de reações sobre o eixo.
Passo 1
A diferença dessa questão para a anterior é que agora a força de ganha duas componentes uma no sentido de e outra no sentido de . De modo que tenhamos agora o seguinte diagrama de forças.
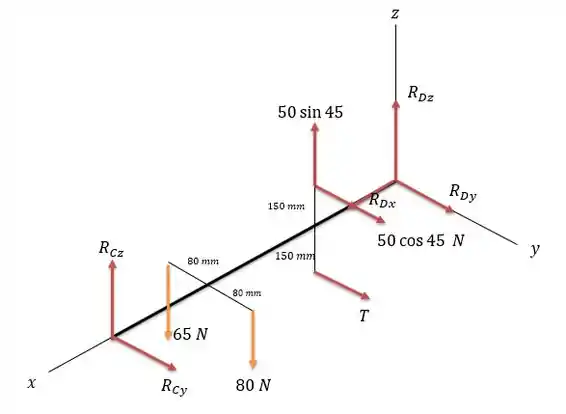
A somatória das forças em continua nos dando:
Passo 2
Em relação ao momento temos que que atua no sentido agora faz momento no eixo em derando momento em , de resto a equação dos momentos agora fica:
Os momentos em :
Agora para os momentos em :
Agora para os momentos em :
Isso nos diz que o sentido da reação é o contrário da que foi desenhada no desenho.
Passo 3
Fazendo a somatória das forças em temos:
E a somatória das forças em :