Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 70
70- Para a viga e o carregamento mostrados nas figuras, trace os diagramas de esforço cortante e de momento fletor, determine os valores absolutos máximos do esforço cortante e do momento fletor.
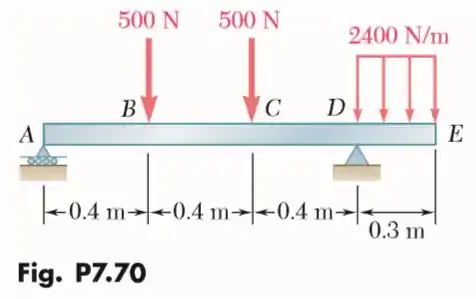
Passo 1
Antes de fazer os diagramas vamos calcular as reações em e .
Sabendo que o carregamento de gerará uma carga total de:
A uma distância de do apoio em .
Isso nos dá um diagrama de forças equivalente igual a:
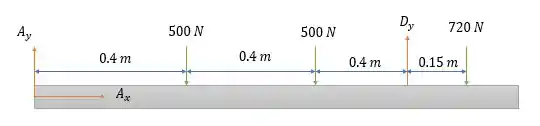
Pela somatória das forças horizontais (e igualando a zero) temos que:
Pela somatória das forças verticais temos:
E pela somatória dos momentos em :
Logo:
Passo 2
Vamos começar fazendo o diagrama da cortante analisando o intervalo de
Pela soma das forças verticais temos:
Agora para :
Fazendo a somatória das forças verticais:
Agora para :
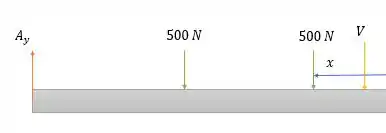
Pela somatória das forças verticais:
Agora para :
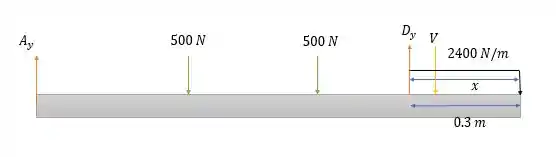
Pela somatória das forças verticais temos:
Onde e nos dando:
Onde se
Nos dando então o seguinte diagrama de cortante.
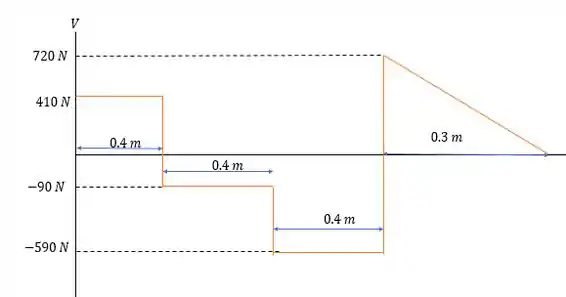
O máximo valor absoluto de cortante vale .
Passo 3
Agora vamos para o diagrama de momento fletor.
Para :
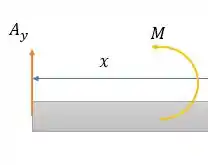
Fazendo a somatória dos momentos nessa barra temos:
Onde para temos:
Para temos
Agora para temos:
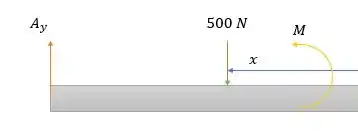
Fazendo a somatória dos momentos temos:
Onde . O que nos dá:
E para nós temos:
Para facilitarmos nossa vida no trecho de vamos transferir para o começo dessa seção o momento resultante e a força resultante vinda das duas seções anteriores.
Pela somatória dos momentos temos:
Onde e , logo:
Dessa forma para temos:
Com esse mesmo raciocínio podemos fazer para :
Fazendo a somatória dos momentos temos:
Onde e o que nos dá:
Com temos , o que faz sentido pois acabou a viga.
O maior valor absoluto de momento que encontramos é , isso pode fazendo a derivada dessa última equação e igualando a zero e por só termos retas antes disso (cujo valores extremos estarão nas extremidades apenas) nos dando o seguinte diagrama de momentos:
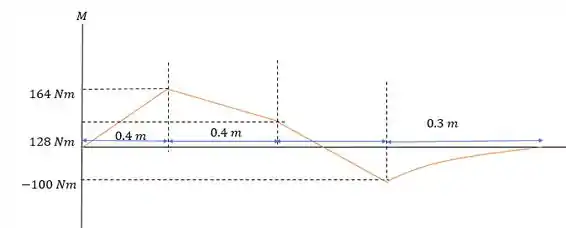
O maior momento absoluto vale: