Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 74
74- Usando o método da Seção , resolva o Problema
Passo 1
Viga do Problema :
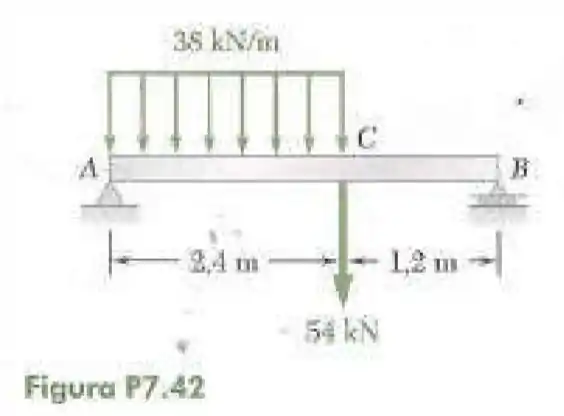
Pede-se:
- Os diagramas do esforço cortante e do momento fletor
- Os valores absolutos e máximos do esforço cortante e do momento fletor
Mesma coisa, vamos encontrar as reações em e sabendo que o carregamento de gera uma força total na barra de:
A uma distância de de , gerando a viga equivalente abaixo.
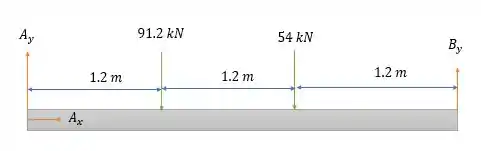
Fazendo a somatória das forças horizontais temos:
Fazendo agora a somatória das forças verticais:
E a somatória dos momentos em :
Dessa forma será:
Passo 2
Dessa forma vamos começar a análise das cortantes e dos momentos fletores na seção :
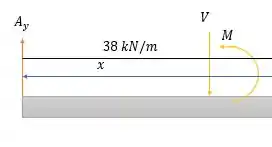
Fazendo a somatória das forças verticais nós temos:
Onde para nós teremos:
E calcular o momento vamos fazer:
E o momento para será:
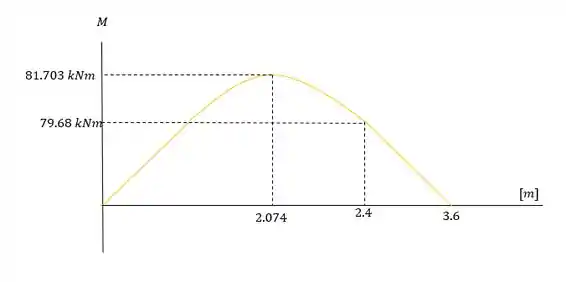
Mas esse será o momento máximo? Não sabemos, vamos derivar a equação que encontramos para garantir.
Essa posição nos dará um momento igual a:
O recomendado é sempre fazer isso em todas as parábolas.
Agora para a seção de :
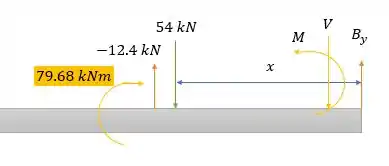
Pela somatória das forças nós temos:
Valor esse que se anula com .
Além de percebermos que o maior valor absoluto da cortante vale:
Agora o valor da somatória dos momentos valerá:
Onde para nós teremos:
Passo 3
Diagrama da cortante:
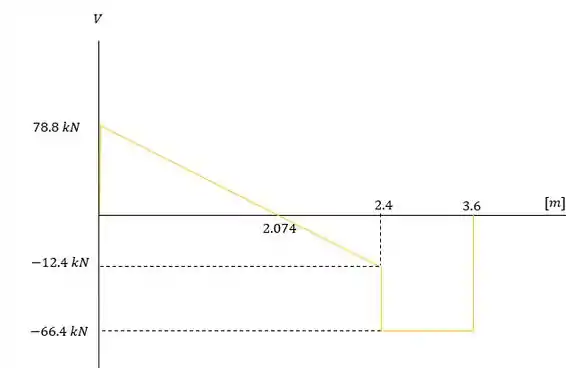
Diagrama do momento fletor:
