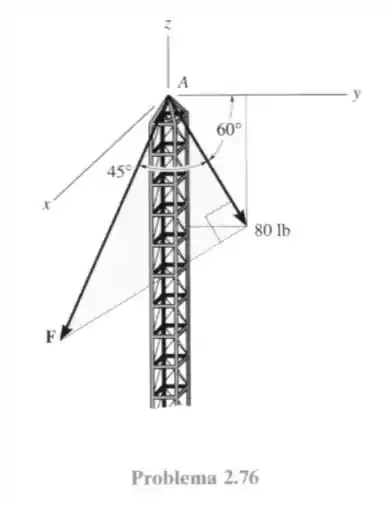
76- A força está aplicada em no topo da torre. Se ela atua na direção mostrada, de modo que um de seus componentes localizado no plano sombreado tem intensidade de , determine sua intensidade e os ângulos diretores coordenados .
Passo 1
Como dito no enunciado a força de que vamos chamar de está somente no plano enquanto a força que chamaremos de é a força só que rotacionada de na direção do eixo . De forma que:
Passo 2
Da mesma forma que a força rotacionou na direção do eixo então faltarão mais para essa força atingir o eixo então representando cartesianamente nós teremos:
Uma abordagem seria ver que a força de é a projeção de no plano e com isso verificar suas componentes nesses dois eixos.
Passo 3
Com essa última informação e sabendo que a intensidade de vale temos os ângulos diretores da força. Que serão calculadas da seguinte forma: