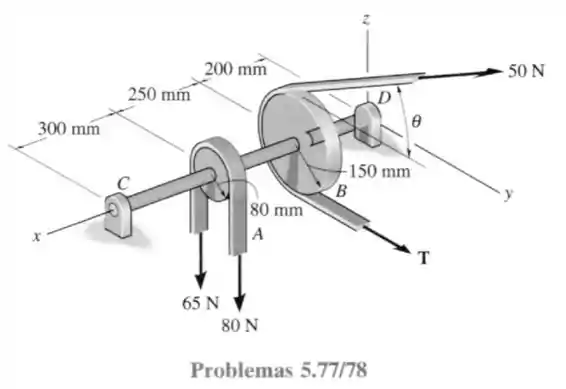
77- Ambas as polias são fixadas no eixo que gira com velocidade angular constante. A potência da polia é transmitida a polia . Determine a força horizontal na correia da polia e os componentes de reação no mancal simples em e no mancal de encosto em , quando . Os mancais estão adequadamente alinhados e exercem apenas forças de reação sobre o eixo.
Passo 1
E aí galera! Vamos para mais uma questão desse livro.
Note que o apoio em resiste a força nos três sentidos, enquanto o apoio em resiste a forças em e . E nenhum deles resiste a nenhum momento (pelo enunciado). De modo a ter o seguinte sistema de forças.
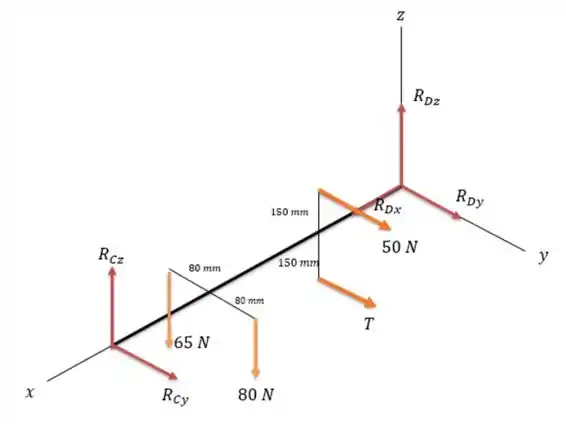
Isso sabendo que então a força na polia encontra-se totalmente no eixo .
E facilmente podemos ver que não existe nenhuma força sendo imposta no eixo então fazendo a somatória das forças em ser nula nós temos:
Passo 2
Vamos calcular os momentos no apoio em , vendo que as forças nas polias e na reação em causam o momento em .
Escolhendo primeiro a somatória dos momentos em serem nulas(causado pelas forças na polia com o eixo e com na distância a ), o que nos dá:
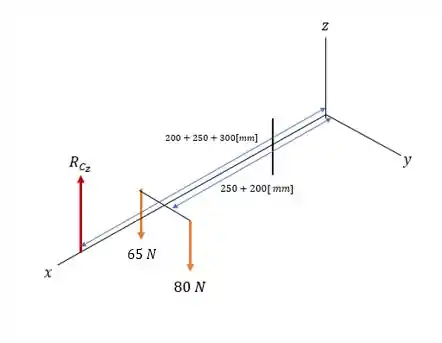
Passo 3
Agora para as somatórias dos momentos em serem nulas(causados somente pelas forças nas polias e com distância ao eixo iguais aos raios das polias):
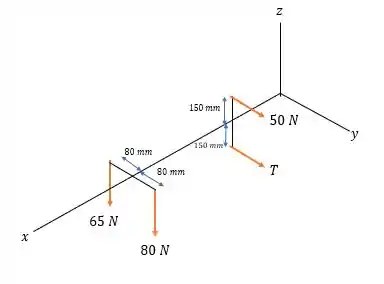
Passo 4
Agora para a somatória dos momentos em serem nulas (causado pela força na polia no eixo e de com o eixo ):

Isso nos diz que o sentido da reação é o contrário da que foi desenhada no desenho acima.
Passo 5
Agora falta encontrar as reações no apoio , além da que foi encontrada no passo 1.

Fazendo a somatória das forças em ser nula nós temos:
Fazendo a somatória das forças em ser nula nós temos:
Isso significa que a força está no sentido contrário ao desenhado no diagrama.