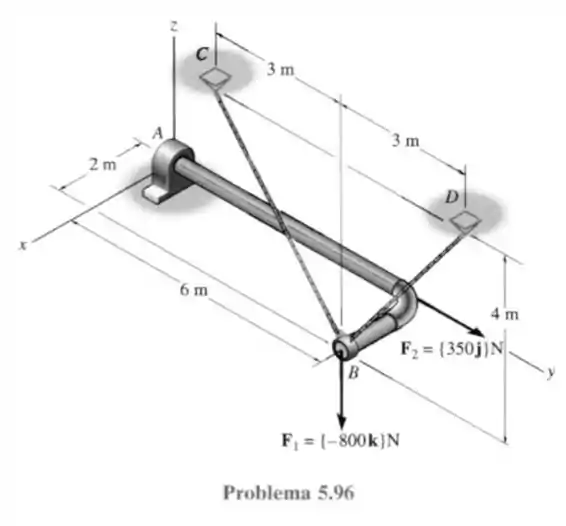
96- Determine os componentes de reação no mancal simples e a força necessária nas cordas e para o equilíbrio da barra.
Passo 1
Esse tipo de mancal fornece uma resistência axial no eixo e no eixo além de resistir ao torque nesses dois eixos. Além de existir a força de tração nos dois cabos. A combinação de todas essas forças surge o diagrama de forças abaixo.
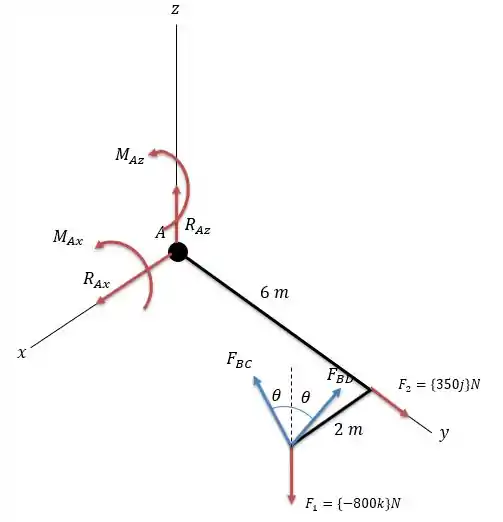
Onde se encontra no triângulo formado entre a corda e os apoios cujo valor vale:
Passo 2
Vamos encontrar vetorialmente as forças e para poder começar a nossa análise.
O ponto se encontra na posição cartesiana igual a:
E os pontos e encontram-se em:
Isso nos dá os seguintes vetores e .
Que terão o mesmo comprimento igual a:
Logo o vetor das duas forças serão iguais a:
Passo 3
Como não temos nenhuma força em podemos dizer pela somatória das forças em que:
Agora a somatória das forças em nos daria que:
E o somatório das forças em :
Passo 4
Agora vamos partir para os momentos exercidos em .
O momento em é causado pelas forças presentes no nó e será igual a zero.
Já que não existe um .
A junção dessa equação com essa:
Nos mostra que
Passo 5
As forças e também exercem momento no eixo de porém quando projetadas em ou seja.
Utilizando essa equação encontramos:
Passo 6
Agora falta o momento que as forças fazem momento na barra de em , para isso vamos utilizar as forças em .
Como descobrimos no passo que:
Logo:
Substituindo :
Passo 7
Agora somente falta descobrir as forças e , para isso basta somente fazer o sistema:
Isso nos dá: