89- Os cabos exercem no poste as forças mostradas na figura. Supondo que o poste é apoiado por uma junta esférica em sua base, determine os componentes das reações em . As forças de e se encontram num plano horizontal.
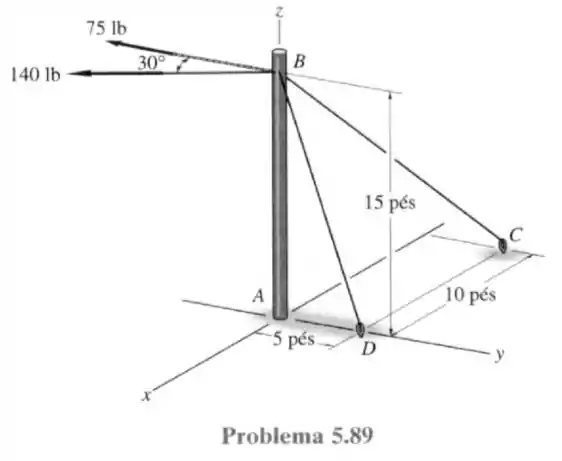
Passo 1
A base do poste exerce resistência nos três eixos, o que faz com que o poste tenha o seguinte diagrama de forças.
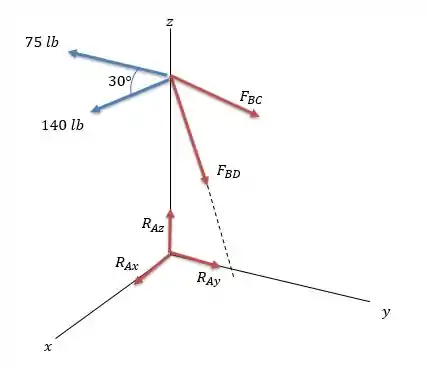
Para resolver essa questão precisamos saber o vetor unitário de e de , então vamos fazer passo a passo:
Posição dos pontos e .
Com isso os vetores e serão:
E ambos terão um tamanho igual a:
Logo os dois vetores unitários serão:
E a força será:
Passo 2
Fazendo a somatória dos momentos na base em temos:
Agora a somatória dos momentos em :
Com isso encontramos:
Passo 3
Agora vamos fazer a somatória das forças:
A somatória em é:
A somatória das forças em :
E a somatória das forças em :