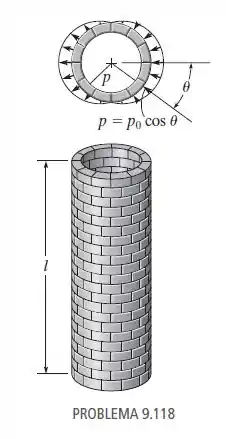
9.118 Uma carga de vento cria uma pressão negativa (sucção) sobre o outro lado, como mostra a figura. Se essa carga de pressão atua uniformemente ao longo do comprimento da chaminé, determine a intensidade da força resultante criada pelo vento.

Se liga só no esquema da questão:

A gente precisa sacar duas coisas:

- A primeira é reparar que a gente vai precisar multiplicar por 2 porque tem dois vetores apontando pra mesma direção.

- A segunda é que a pressão não é constante, ela varia com o ângulo .

Então a pressão em fica:

E a pressão em fica:

Outra coisa que precisamos definir é o , né?

Repara que a área é a lateral do cilindro, então ficamos com:

E repara também que os limites de integração vão de até . (já que só o varia, o não varia.

Showww... Agora é só a gente jogar nas integrais e resolver:

- Pra :

E resolvendo essa integral: (como )

- Pra

Resolvendo a integral:

Fazendo, por substituição, :

E voltando pra nossa integral:

Então a força resultante vai ser:

Ufaaa... Essa deu um trabalhinho, mas foi. Bora pra próxima??