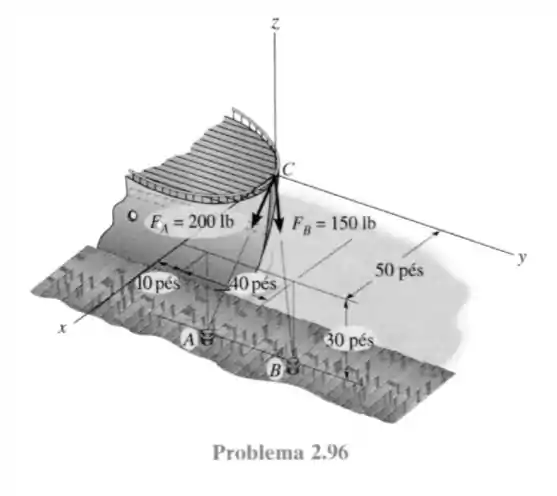
96- Os dois cabos de amarração exercem forças na popa de um navio, como mostrado na figura. Represente cada força como um vetor cartesiano e determine a intensidade e a direção da resultante.
Passo 1
A figura ficou um pouco poluída mas conseguimos encontrar as posições de cada ponto em relação a origem no ponto .
As coordenadas são vistas utilizando o plano então veja elas de cima.
Passo 2
Agora temos que calcular a equação do vetor e , começando de .
E seus comprimentos valem:
Passo 3
Por conta disso vamos calcular os vetores unitários dos dois vetores de posição:
Passo 4
Como a intensidade da força que corre o cabo vale então temos o vetor de força ao multiplicar a intensidade pelo vetor unitário desse cabo:
Com o mesmo raciocínio temos :
Passo 5
Se somarmos as duas forças teremos a força resultante:
Esse vetor resultante terá uma intensidade igual a:
Passo 6
Utilizando o vetor da força resultante e intensidade teremos os ângulos diretores do vetor: