60- A viga uniforme tem peso , comprimento e é apoiada por um pino em e um cabo em . Determine os componentes horizontal e vertical da reação em e a tensão necessária no cabo para manter a viga na posição mostrada na figura.
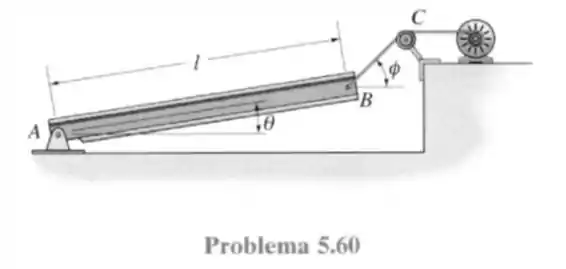
Passo 1
O sistema de forças na viga pode ser representado da seguinte forma.
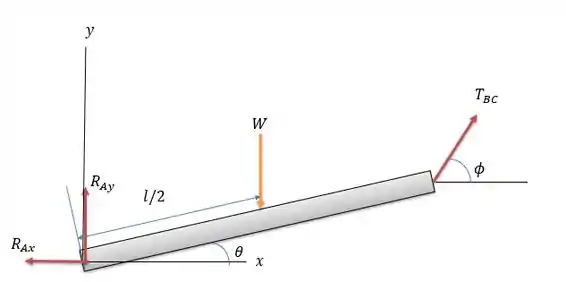
Para encontrar a força em função do peso vamos calcular os momentos em , para isso vamos precisar da viga equivalente abaixo.
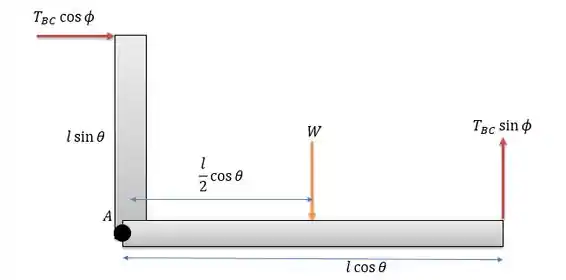
E como ao pino em não oferece resistência ao torque então a somatória dos momentos será zero. E a força inclinada gera momento na distância vertical e na distância horizontal.
Considerando o sentido horário como positivo então:
Dessa forma temos:
Porém logo:
Passo 2
Agora para encontrar as reações no apoio temos que fazer a somatória nos eixos:
Fazendo a somatória em temos:
E a somatória das forças em será:
Substituindo :