Agora, faça o mesmo, mas considere que .
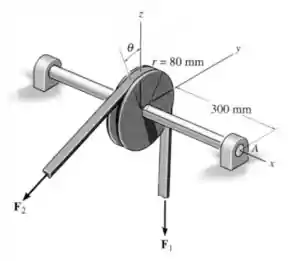
Questão Anterior: A correia que passa pela polia é submetida às forças e , cada uma com intensidade de . A força atua na direção . Substitua essas forças por uma força e momento equivalentes no ponto . Expresse o resultado na forma de vetor cartesiano. Considere , de forma que atue na direção .
Passo 1
No caso em que o ângulo , podemos escrever a força da seguinte forma:
E a força aponta na direção de , então:
Então a força resultante agindo sobre o sistema é:
Passo 2
Quando substituirmos esse par de forças por uma única força aplicada no ponto , o momento resultante em relação a esse ponto será nulo.
Então, se queremos manter o mesmo efeito final no sistema, precisamos aplicar um novo momento, que “reponha” o que foi perdido com a mudança nas forças.
Vamos ver qual era o momento total em relação ao ponto :
Precisamos escrever esses vetores e , que dão a posição dos pontos de aplicação das forças em relação ao ponto . Para isso, dê uma olhada nos desenhos:
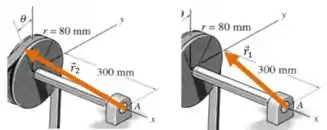
Em comparação com o problema anterior, o vetor passará a ter uma pequena componente na direção , pois ele deve mirar no ponto em que a força é tangente à roda:
Passo 3
Ok, então voltando à nossa equação para o momento resultante:
Vamos escrever esses produtos vetoriais como determinantes:
E para o outro produto:
Então:
Resposta
O sistema pode ser substituído por uma força e por um momento .