Substitua os dois torsores que atuam na estrutura de tubos por uma força resultante e um momento equivalentes no ponto .
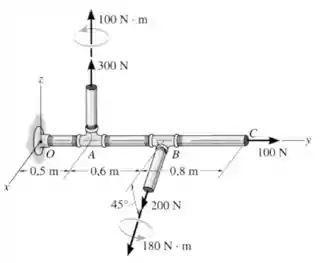
Passo 1
Vamos começar escrevendo as forças em forma vetorial:
E então podemos calcular a força resultante:
Passo 2
Agora vamos calcular o momento total em relação ao ponto . Para isso temos que considerar tanto os momentos das forças quanto os que já estão representados no desenho:
Podemos escrever os dois últimos termos apenas olhando para o desenho do enunciado:
E para os dois primeiros termos, precisamos prieira escrever os dois vetores de posição e :
A força de ( tem momento nulo, já que sua linha de ação passa pelo ponto , então já podemos exlcuir esse termo da nossa equação:
Agora vamos substituir tudo na fórmula dos momentos, escrevendo o produto vetorial como um determinante:
Resposta
O sistema pode ser substituído por uma força e por um momento .