Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 146

Um arame de alumínio com 0,033   l b / f t de massa por unidade de comprimento é usado para formar o círculo e os membros retilíneos mostrado na figura. Determine o momento de inércia de massa do conjunto em relação a cada um dos eixos coordenados.

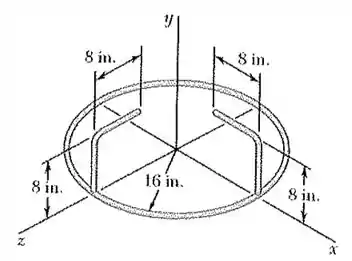
Passo 1

Primeiro, vamos pegar o numero de massa de cada elemento! Vamos considerar cada elemento como mostrado abaixo na figura!

m = W g = 1 g W L a l L

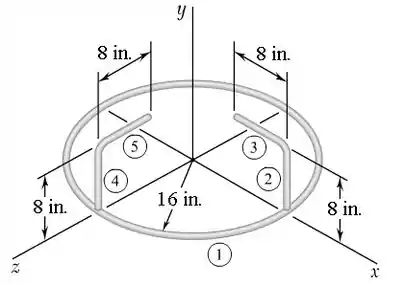
Logo,

m 1 = 1 32.2 0.0 33 × 2 π × 1 6 × 1 12 = 8.5857 × 10 - 3 l b ⋅ s 2 / f t

A parte boa é que os elementos 2,3,4 e 5 são iguais, então calculando a massa de um já garante o dos outros.

m 2 = m 3 = m 4 = m 5 = 1 32.2 × 0.033 × 8 × 1 12 = 0.6832   l b ⋅ s 2 \ f t

Passo 2

Agora que temos as massas, vamos aplicar o teorema dos eixos pararelos, para achar os momentos de inercia de massa de cada elemento e soma-los!

I x = I x 5 + I x 4 + I x 3 + I x 2 + I x 1

= 1 2 ( 8.5857 × 10 - 3 ( 16 ) × 1 12 2

+ 1 3 ( 0 . 6832   ( 8 ) × 1 12 2

+ 0 + ( 0.6832   ( 8 ) × 1 12 2

+ 1 12 ( 0.6832   8 + ( 0.6832   4 2 + 16 2 × 1 12 2

+ 1 12 ( 0.6832   8 + ( 0.6832   8 2 + 1 2 2 × 1 12 2

= 10.3642 × 10 - 3   l b ⋅ f t ⋅ s 2

Passo 3

Calculando I y :

I y 2 = I y 4

I y 3 = I y 5

I y = I y 5 + I y 4 + I y 3 + I y 2 + I y 1

= ( 8.5857 × 10 - 3 ( 16 ) × 1 12 2

+ 2 ( 0.6832   ( 16 ) × 1 12 2

+ 2 1 12 ( 0.6832   8 + ( 0.6832   12 2 × 1 12 2

= 1 9 . 1097 × 10 - 3   l b ⋅ f t ⋅ s 2

Passo 4

Pela simetria, I x = I z , logo:

I x = 10.3642 × 10 - 3   l b ⋅ f t ⋅ s 2

I y = 19.1097 × 10 - 3   l b ⋅ f t ⋅ s 2

I z = 10.3642 × 10 - 3   l b ⋅ f t ⋅ s 2

Resposta

I x = 10.3642 × 10 - 3   l b ⋅ f t ⋅ s 2

I y = 19.1097 × 10 - 3   l b ⋅ f t ⋅ s 2

I z = 10.3642 × 10 - 3   l b ⋅ f t ⋅ s 2

Ver Outros Exercícios desse livro