Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 70

Determinar por integração direta o produto de inércia da superfície dada em relação aos eixos x e y .

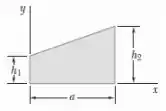
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Desenhando o diagrama, temos:

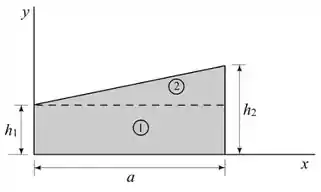
O produto de inércia do retângulo I x y 1 = x - y - A 1

I x y 1 = a 2 h 1 2 a h 1

I x y 1 = a h 1 2 4

Passo 2

O produto de inércia do triângulo é dado por:

I x y 2 = I - x ' y ' + x - y - A

I x y 2 = - 1 72 a 2 h 2 - h 1 2 + 2 a 3 h 1 + h 2 - h 1 3 1 2 a h 2 - h 1

Resolvendo e simplificando, temos que:

I x y 2 = a 2 72 h 2 - h 1 17 h 1 + 7 h 2

Passo 3

O produto de inércia da área sombreada será:

I x y = I x y 1 + I x y 2

Subsituindo os valores, temos:

I x y = a h 1 2 4 + a 2 72 h 2 - h 1 17 h 1 + 7 h 2

Resposta

I x y = a h 1 2 4 + a 2 72 h 2 - h 1 17 h 1 + 7 h 2

Ver Outros Exercícios desse livro