Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 172

Para a armação de arame do problema indicado, determine o momento de inércia de massa da armação em relação ao eixo que passa pela origem caracterizado pelo vetor unitário λ = ( - 3 i - 6 j + 2 k ) / 7 . Problema 9.146.

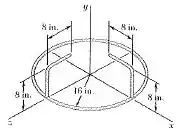
Passo 1

Antes vamos separar cada componente, de tal modo que:

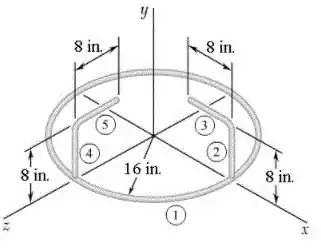
Passo 2

Agora, que separamos cada parte, vamos computar a massa de cada componente. Dessa maneira,

m = W g = 1 g W L A L L

Então,

m 1 = ( 0.033   l b / f t ) ( 2 π * 16 i n ) 32.2 f t / s 2 * 1 f t 12 i n

m 1 = 8.5857 * 10 - 3 l b * s 2 / f t

m 2 = m 3 = m 4 = m 5 = ( 0.033   l b / f t ) ( 8   i n ) 32.2 f t / s 2 * 1 f t 12 i n

m 2 = m 3 = m 4 = m 5 = 0.6832 * 10 - 3   l b * s 2 / f t

Passo 3

Certo! Agora observe que os produtos de inércia centrais I x ' y ' , I y ' z ' e I z ' x ' são zeros, por causa da simetria. Como também

x - 1 =   x - 4 = x - 5 = 0

y - 1 = 0

z - 1 =   z - 2 = z - 3 = 0

Então os produtos de inércia são:

Produto de inércia xy

I x y = ∑ I x ' y ' + m x - y -

I x y = m 2 x - 2 y - 2 +   m 3 x - 3 y - 3

I x y = 0.6832 * 10 - 3   l b * s 2 f t   16 12 f t 4 12 f t + 0.6832 * 10 - 3 l b * s 2 / f t     12 12 f t 8 12 f t

I x y =   0.75911 * 10 - 3   l b * f t * s 2

Produto de inércia yz, por simetria é igual ao do xy. Portanto

I y z = I x y

I y z =   0.75911 * 10 - 3   l b * f t * s 2

Produto de inércia zx

I z x =   ∑ I z ' x ' + m z - x - = 0

Passo 4

Da solução do Problema 9.146 obtivemos

I x = I z = 10.3642 * 10 - 3 l b * f t * s 2

I y = 19.1097 * 10 - 3 l b * f t * s 2

Passo 5

Agora com os momentos de inércia dos eixos e os produtos de inércia calculados, só basta substituir na equação abaixo que teremos nossa resposta

I O L = I x λ x 2 + I y λ y 2 + I z λ z 2 - 2 I x y λ x λ y - 2 I y z λ y z - 2 I z x λ z λ x

A questão nos oferece

λ = ( - 3 i - 6 j + 2 k ) / 7

Portanto

I O L = 10.3642 - 3 7 2 + 19.1097 - 6 7 2 + 10.3642 2 7 2 - 2 0.75911 - 3 7 - 6 7 - 2 0.75911 - 6 7 2 7 * 10 - 3   l b * f t * s 2

I O L = 16.61   l b * f t * s 2

Resposta

I O L = 16.61   l b * f t * s 2

Ver Outros Exercícios desse livro