Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 141

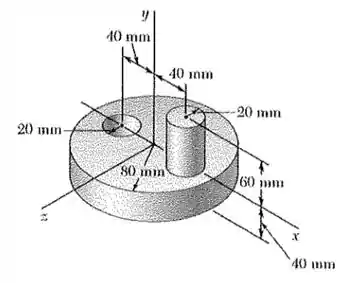
Determine o momento de inercia de massa do elemento de maquina de aço mostrado n a figura em relação ao eixo y . (O peso especifico do aço é especifico do aço é 77.000   N / m 3 ).

Passo 1

Das questões de momento de inércia de massa, essa é uma das mais grandinhas. Mas não significa que ela é difícil! Vamos trabalhar cada parte com calma e vai dar tudo certo hahaha! 😊 Primeiro, vamos pegar o numero de massa de cada elemento! Vamos considerar como elemento 1 o nosso disco, elemento 2 o cilindro que está em cima do disco, e elemento 3 o buraco!

m = ρ V

m 1 = 7850 π 0.08 2 ⋅ 0.04 = 6.31334   k g

m 2 = 7850 π 0.02 2 ⋅ 0.06 = 0.591 88   k g

m 3 = 7850 π 0.02 2 ⋅ 0.04 = 0.39458   k g

Passo 2

Agora que temos as massas, vamos aplicar o teorema dos eixos pararelos, para achar a os momentos de inercia de massa de cada elemento e soma-los! Usando a figura 9.28 pode nos ajudar!

I x = I x 1 + I x 2 - I x 3

= 1 12 6.31334 3 0.08 2 + 0.04 2 + 6.31334 0.02 2

+ 1 12 0.59188 3 0.02 2 + 0.06 2 + 0.59188 0.03 2

- 1 12 0.39458 3 0.02 2 + 0.04 2 + 0.39458 0.02 2

= 13.988 × 10 - 3   k g ⋅ m 2

Passo 3

Vamos repetir o mesmo procedimento, agora pra o eixo y .

I y = I y 1 + I y 2 - I y 3

= 1 2 6.31334 0.08 2

+ 1 2 0.59188 0.02 2 + 0.59188 0.04 2

- 1 2 0.39458 0.02 2 + 0.39458 0.04 2

= 20.55783 × 10 - 3   k g ⋅ m 2

Passo 4

Vamos repetir o mesmo procedimento, agora pra o eixo z .

I z = I z 1 + I z 2 - I z 3

= 1 12 6.31334 3 0.08 2 + 0.04 2 + 6.31334 0.02 2

+ 1 12 0.59188 3 0.02 2 + 0.06 2 + 0.59188 [ 0.04 2 + 0.03 2 ]

- 1 12 0.39458 3 0.02 2 + 0.04 2 + 0.39458 [ 0.04 2 + 0.02 2 ]

= 14.30368 × 10 - 3   k g ⋅ m 2

Resposta

I x = 13.988 × 10 - 3   k g ⋅ m 2

I y = 20.55783 × 10 - 3   k g ⋅ m 2

I z = 14.30368 × 10 - 3   k g ⋅ m 2

Ver Outros Exercícios desse livro