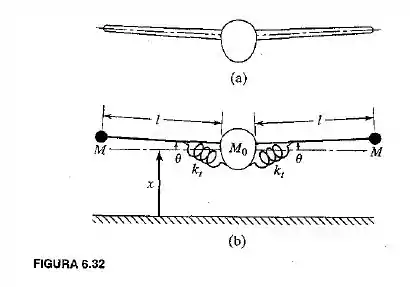
Quando um avião (Figura 6.32a) sofre vibrações simétricas, a fuselagem pode ser idealizada como uma massa central concentrada , e as asas podem ser modeladas como barras rígidas que suportam massas em suas extremidades, como mostra a Figura 6.32b. A flexibilidade entre as asas e a fuselagem pode ser representada por duas molas torcionais, cada uma com rigidez .
- Deduza as equações de movimento do avião utilizando equações de Lagrange com como coordenadas generalizadas.
- Determine as frequências naturais e formas modais do avião.
- Determine a constante elástica torcional de modo que a frequência natural de vibração, em modo torcional, seja maior do que 2 Hz quando .
Passo 1
Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?
- Inicialmente, vamos definir que nossas coordenadas generalizadas são essas aqui .
- Galera, uma vez que por definição das oscilações harmônicas, nós temos , as equações de movimento vão ser as seguintes:
- No terceiro item, nós temos que para
Da fórmula da energia cinética, nós encontramos o seguinte:
Da fórmula da energia potencial, nós vamos ter:
Dito isso, podemos concluir, usando as equações de Lagrange, que para a primeira coordenada nós temos:
Já para a segunda coordenada, teremos:
Por fim, teremos a solução com as equações de Lagrange se tornando:
Passo 2
O que nos leva para a equação de frequência:
Ou seja:
Das equações do movimento escritas anteriormente, nós tiramos que:
E quando
O que nós encontramos aqui corresponde a translação de corpo rígido na direção x(vertical).
E quando
Passo 3
Pelos valores propostos, substituindo para , essa inequação se torna o seguinte:
Resposta
Ei, a resposta está no passo a passo :)