Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 106
A barragem de concreto por ‘gravidade’ é mantida por seu próprio peso. Se a densidade do concreto é , e a água tem uma densidade de , determine a menor distância em sua baseque impedirá que a barragem tombe em torno de sua extremidade . A barragem tem uma largura de .
Passo 1
Olá, querido! Queremos o valor de para a barragem ficar paradinha. Então o que a gente vai fazer é achar as forças atuando na barragem e usar as equações de equilíbrio.
Um cara chamado Pascal enunciou uma vez que, um fluido em repouso cria uma pressão em um ponto que é a mesma em todas as direções.
A intensidade de , medida como uma força por área unitária, depende do peso específico ou densidade de massa do fluido e da profundidade do ponto a partir da superfície do fluido. Podemos escrever a expressão da pressão como:
A barragem tem metros de largura, beleza? Tendo isso em mente, vamos descobrir a intensidade de carga que a água causa na barragem:
Passo 2
A carga que a água faz sobre a barragem é uma carga distribuída que tem formato de triângulo. Onde o ponto mais alto do triângulo ocorre em e vale . Para posicionar esse triângulo, a gente coloca a base dele paralela a parede da barragem e a ponta dele coincidindo com a superfície da água.
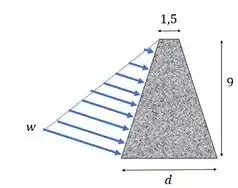
A força resultante é dada pela área desse triângulo. A altura dele é . A altura a gente precisa achar. Podemos usar pitagoras
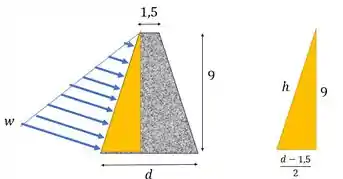
A força resultante fica:
Essa força atua através do centroide da área. Que é . Pela geometria do triângulo, ele está em:
Em relação a vertical. Vemos no desenho a seguir que acontece alho análogo na horizontal
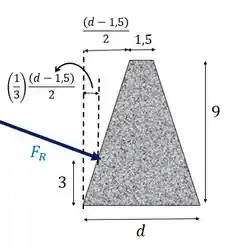
Passo 3
Nos falta ainda saber o valor do peso da barragem, . Logo, o valor de será escrito da seguinte forma:
Onde é a largura da barragem, é densidade dela, é a gravidade e é a área da seção transversal que na figura vemos que é um trapézio e dada por
Substituindo os valores na expressão, temos:
Passo 4
Nosso DCl da barragem fica:
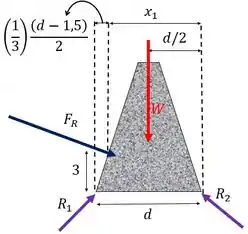
Aqueles são as reações do solo para segurar a barragem. Mas lembra que a gente quer o mínimo. Isso ocorre na eminência de rotação. Como a água tende a girar a barragem no sentido horário, temos que nesse momento .
Aí para achar , a gente pode fazer o momento nesse ponto de aplicação de . Aí a gente não precisa se preocupar em acha-lo.
Mas para fazer o momento, vamos decompor na vertical e na horizontal. Vamos voltar a usar aquele triângulo amaralelo
Passo 5
Olhando nosso DCL, vemos que
Agora que temos todas as informações de forças atuando na barragem, vamos calcular o momento no ponto de aplicação de . O somatório dos momentos para sistemas em equilíbrio é igual a zero. Assim, adotando como sentido positivo anti-horário, temos:
Fazendo a distributiva, a gente cai numa equação do segundo grau. Resolvendo essa equação e escolhendo a solução positiva (já que é uma distância, e distância são positivas), achamos:
Resposta
A menor dimensão que impedirá que a barragem tombe é: