Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas fundamentais - Ex. 10
Localize o centroide da área da seção transversal.
Passo 1
Fala galerinha do RespondeAí, tudo beleza?
Saca só, pra gente fazer esse exercício aqui, a primeira coisa que devemos fazer é dividir nossa figura em outras figuras mais simples, nesse caso podemos dividir da seguinte maneira:
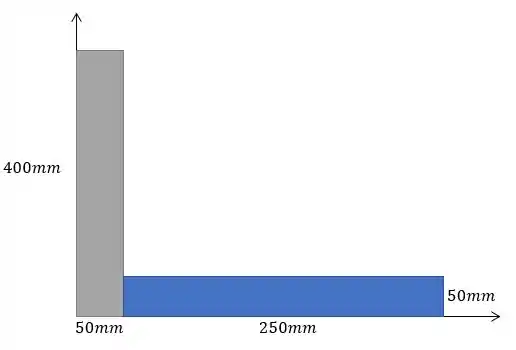
Agora podemos calcular as posições do centroide de cada uma das figuras separadamente. Assim poderemos aplcar as equações para o centroide de uma figura composta, dadas como:
Iradoso, então bora lá.
Passo 2
Se a gente fizer uma tabelinha com os valores de cada figura, vamos obter o seguinte:
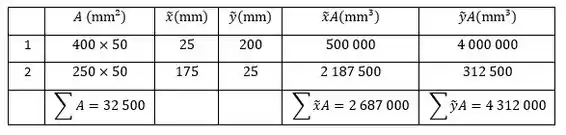
Sendo assim, vamos obter que no eixo , a coordenada no centroide da figura será:
E para o eixo :
Resposta
Exercícios de Livros Relacionados
Determine a profundidade h do furo de 100m m de diâmetro feito na base do cone de modo que o centro de massa do sólido resultante esteja localizado em z -=115m m . O material tem densidade de 8M g / m
A placa composta é feita de segmentos de aço ( A ) e latão ( B ) . Determine a massa e a localização ( x - ,y - ,z - ) de seu centro de massa G . Considere ρ a ç o = 7,85M g / m 3 ç e ρ l a t ã o = 8,
Determine a distância z - até o centroide do sólido que consiste em um cone com um furo de altura h=50m m feito em sua base.
Determine a localização y do centroide C da viga com a seção transversal mostrada.
Localize o centroide y da seção transversal da viga montada a partir de uma canaleta e de uma placa. Suponha que todos os cantos sejam “vivos” e desconsidere o tamanho da solda em A.