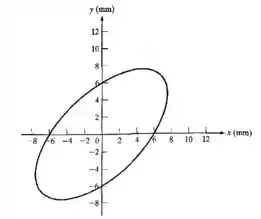
A base de um compressor de ar está sujeita a movimentos harmônicos (com a mesma frequência) em duas direções perpendiculares. O movimento resultante exibido na tela de um osciloscópio é como o mostrado na Figura 1.87. Determine as amplitudes de vibração nas duas direções e a diferença de fase entre elas.
Passo 1
Faaala pessoal, tudo bem? Vamos lá pra mais uma questão e vai dar certo.
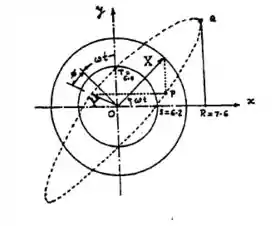
Temos que a equação (E.1) para movimento resultante é igual a:
Substituindo o , a (E.1) se reduz a:
E, portanto, chegamos na (E.2) a seguir, com resultado representado por “OS” na figura:
Novamente, substituindo o , a (E.1) se reduz a:
Dessa vez, chegamos na (E.3) a seguir, com resultado representado por “OT” na figura:
Passo 2
Considerando as 3 equações obtidas no passo 1, a (E.1), a (E.2) e a (E.3), conseguimos ver que “OR” na figura, vai ser representado pelo resultado da equação (E.4) a seguir:
Dito isso, temos a (E.5) a seguir:
Das (E.2) e (E.4), encontramos que:
Das (E.3) e (E.5), obtemos: