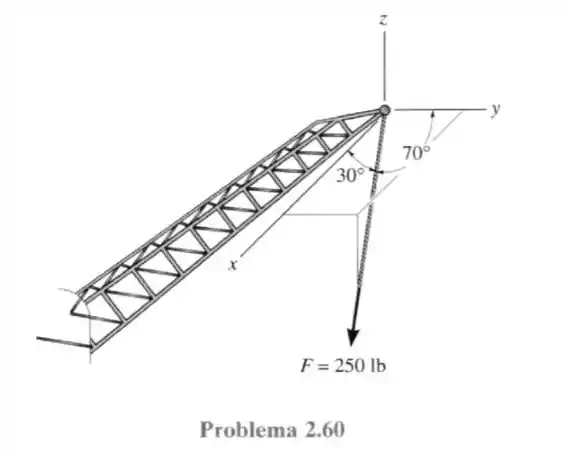
60- O cabo da extremidade da lança do guincho exerce uma força de sobre a lança, como mostrado. Expresse como um vetor cartesiano.

A questão nos informa os ângulos diretores da força em relação a e ou seja e . Então vamos encontrar pela relação fundamental.

Aplicando a relação fundamental temos:

Logo:

Pois para o cosseno ser positivo temos um ângulo no primeiro quadrante e outro no segundo quadrante. Como a força está com sentido contrário a de logo podemos dizer o ângulo é de .