A cápsula espacial tem uma massa de , centro de massa em , e raios de giração em relação a seu eixo de simetria (eixo ) e seus eixos transversais (eixo ou ) de e , respectivamente. Se a cápsula tem a velocidade angular mostrada, dtermine sua precessão e rotação Indique se a precessão é regular ou retrógrada. Também, desenhe o cone do espaõ e o cone do corpo para o movimento.
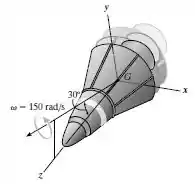
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A única força agindo na capsula espacial é a do seu próprio peso. Portanto:
Com estes dados, temos que:
Dividindo as equações temos que:
E:
Usando estes resultados, temos que:
E: