Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 27

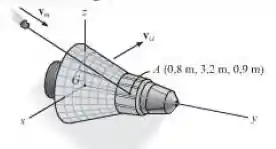
A cápsula espacial tem uma massa de 5   M g e os raios de giração são k x = k z = 1,30   m e k y = 0,45   m . Se ela se desloca com uma velocidade v G = 400 j + 200 k   m / s , calcule sua velocidade angular logo após ela ser atingida por um meteorito tendo uma massa de 0,80   k g e uma velocidade v m = - 300 i + 2 00 j - 15 0 k   m / s . Suponha que o meteorito se embute na cápsula no ponto A e que a cápsula inicialmente não tem velocidade angular.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos aplicar a conservação da quantidade de movimento angular com relação ao centro de massa da capsula em G . A conservação é dada por:

H G 1 = H G 2

r G A × m m v m = I G ω

Observando a figura, temos que:

r G A = ( 0,8 i + 3,2 j + 0,9 k )

Portanto:

0,8 i + 3,2 j + 0,9 k × 0,8 - 300 i + 2 00 j - 15 0 k = I G ω

Vamos resolver o produto vetorial:

0,8 i + 3,2 j + 0,9 k × 0,8 - 300 i + 2 00 j - 15 0 k

det ⁡ i 0,8 - 240     j 3,2 160     k 0,9 - 120

- 120 3,2 i + - 240 0,9 j + 160 0,8 k - [ 160 0,9 i + - 120 0,8 j + - 240 3,2 k )

- 528 i + - 120 j + 896 k

Sabemos que I G = m k 2 .

Logo:

I G ω = I G x ω x i + I G y ω y j + I G z ω z k

I G ω = m k x 2 ω x i + m k y 2 ω y j + m k z 2 ω z k

I G ω = 5000 1,3 2 ω x i + 5000 0,45 2 ω y j + 5000 1,3 2 ω z k

I G ω = 8450 ω x i + 1012,5 ω y j + 8450 ω z k

Agora já temos todos os elementos que precisamos pra encontrar a velocidade angular:

- 528 i + - 120 j + 896 k = 8450 ω x i + 1012,5 ω y j + 8450 ω z k

8450 ω x = - 528

ω x = - 0,06249   r a d / s

1012,5 ω y = - 120

ω y = - 0 , 11852   r a d / s

8450 ω z = 896

ω z = 0 , 1060   r a d / s

Logo:

ω = - 0,06249 i - 0,11852 j + 0,1060 k   r a d / s

Resposta

ω = - 0,06249 i - 0,11852 j + 0,1060 k   r a d / s

Ver Outros Exercícios desse livro