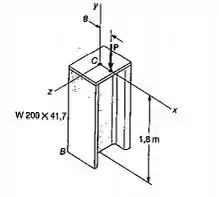
Uma carga axial P é aplicada em um ponto localizado sobre o eixo x, a uma distância e=15,2mm do eixo geométrico do perfil laminado de aço W200x41,7 da coluna BC.
Sabendo-se que a coluna está livre em seu topo C e engastada em sua base B e que =250MPa e E=200GPa, determinar a carga admissível P se um coeficiente de segurança
em relação ao escoamento, de 2,5 é desejado.(Sugestão: Como o coeficiente de segurança deve ser aplicado á P, e não as tensões, usar a Fig. 11.23 para determinar Pe.)
Passo 1
Fala aí pessoal, bora resolver mais uma de equação da secante?
Vamos começar o problema anotando alguns valores úteis das tabelas dos perfis de abas largas e pegando par antes de pegar lá sei que é confuso saber para qual eixo a gente vai analisar o escoamento mas um jeito de não se confundir é lembrar de como a gente olhava pra tensão de flexão na seção, vamos olhar um desenho.
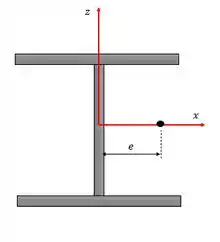
Se a excentricidade está ao longo do eixo , a coluna vai tentar girar em torno de vai ser a tendência do momento fletor, portanto a gente vai pegar os valores para . Nas tabelas do livro a direção aparece como direção e a direção aparece como direção .
O momento de inércia para :
O raio de giração em .
A área da seção transversal:
E o ponto do centro até a fibra mais tracionada ou comprimida é a metade da largura da mesa:
O problema nos pede a carga para o coeficiente de segurança de 2,5 ao escoamento lembrando que:
E a gente já viu nesse capítulo que o jeito de calcular o peso que leva ao escoamento por conta da excentricidade é calculado usando nossa querida equação da secante que para o escoamento a gente faz
Mas e aí, temos uma equação meio complexa né, como a gente vai isolar aquele do argumento da secante? Temos duas opções, a primeira é usar um gráfico e pegar para alguns coeficientes o valor de Pe/A, a outra é usar algum método de encontrar raízes. Vamos seguir de gráfico aqui pois será mais simples.
Passo 2
O próprio problema nos diz para usarmos a figura 11.23 e é o que faremos, vamos dar uma analisada na figura.
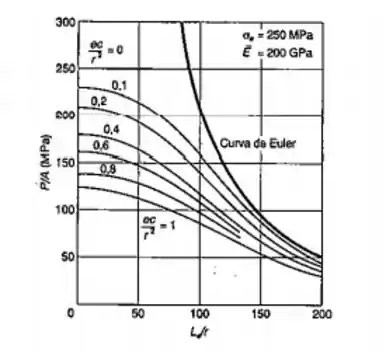
Repare o seguinte, com alguns índices podemos pegar o nosso ponto P/A no gráfico vamos encontrar o índice de esbeltez e o outro parâmetro e achar o nosso ponto. É dito no enunciado que a coluna é engastada e livre, sendo assim o coeficiente de flambagem é
Então o índice de esbeltez será:
E o nosso outro parâmetro é:
Agora é um trabalho aproximado, você pode usar uma régua pra fazer isso, vamos pegar ponto do índice de esbeltez encontrado e traçar uma reta vertical dali subimos até a curva do segundo parâmetro, como no nosso caso caiu entre duas curvas podemos pegar um ponto no meio e traçar uma reta horizontal para encontrar P.
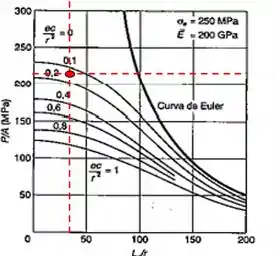
Pelo gráfico temos aproximadamente:
Substituindo a área e isolando :
Em
E como:
Temos: