Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 49
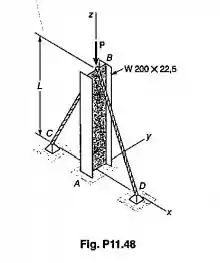
Um perfil laminado de aço W200x22,5 é usado com o apoio fixo e os cabos mostrados no arranjo do prob 11.48. Sabendo-se que L=7,2m, determinar a carga centrada admissível, P se um coeficiente de segurança de 2,2 é desejado. Usar E=200GPa
Passo 1
E aí, vamos pra mais um de flambagem?
Primeiro de tudo, vamos catar nas tabelas do final do livro alguns valores que serão muito úteis. Selecionamos a tabela de perfis de abas largas e para o perfil mostrado W200x22,5 temos:
Para o eixo :
E para o eixo :
Esse exercício traz pra gente o conceito de coeficiente de flambagem e flambagem para dois planos diferentes aqui a chave pra resolver é analisar o que acontece em cada eixo de flambagem, então vamos desenhar:
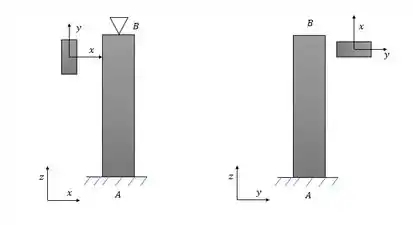
Olhando o nosso desenho a gente pode analisar bem as condições de contorno. No plano a possibilidade de flambagem em torno de é combatida por um apoio e um engaste e no plano apenas o engaste entra em cena.
Definidos nossos parâmetros vamos avaliar o eixo fraco usando um outro parâmetro chamado de índice de esbeltez que é dado por:
O maior índice de esbeltez vai nos dar o eixo mais fraco.
Onde:
E depois calcularemos o peso crítico usando:
E por fim o peso admissível com a relação:
Passo 2
Então vamos definir agora o que a gente vai usar para cada caso, para o plano temos um engaste e um pino o que nos dá:
E como é a iminência de flambar em torno de :
Para o plano coluna engastada e livre que nos dá:
E como é avaliada a iminência de flambar em torno de .
Enfim vamos avaliar qual o maior índice de esbeltez:
E para com
Então o eixo é o eixo fraco agora podemos calcular o peso crítico para esse eixo.
Passo 3
Calculando enfim o peso crítico para , temos:
Substituindo:
E enfim lembrando que: