Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 76
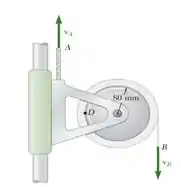
O carretel de fita e sua estrutura de apoio são puxados para cima com uma velocidade . Sabendo que a extremidade B da fita é puxada para baixo com velocidade de e que, no instante mostrado na figura, a espessura total da fita no carretel é de , determine (a) o centro instantâneo de rotação do carretel, (b) a velocidade do ponto D do carretel.
Passo 1
Questão 76 agora, meus chapas!
Bom! O enunciado nos fornece o valor da velocidade com que o carretel é puxado para cima. Ela é igual à...
E nos diz também a velocidade angular do carretel, bem como seu sentido de giro...
Dito isso, vamos fazer um esboço do problema...
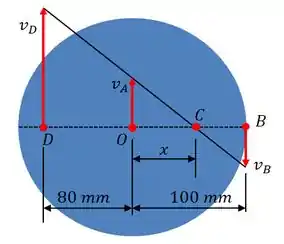
Passo 2
a) Considerando que está posicionado no centro de massa do carretel. Podemos obter o que a gente quer por semelhança de triângulos, que é a distância entre e .
Temos que...
Logo, podemos obter como igual à...
Passo 3
b) Belezinha! Agora, vamos obter as velocidades do ponto .
Por semelhança de triângulo, temos que...
Pronto! Terminamos por hoy! Hasta la vista!
Resposta
a)
b)