Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 47

O carro se desloca em torno de uma estrada curva de raio ρ de tal maneira que seu centro de massa tem uma velocidade constante de v G . Escreva as equações de movimento rotacional em relação aos eixos x ,   y ,   z . Suponha que os seis momentos e produtos de inércia do carro em relação a esses eixos são conhecidos.

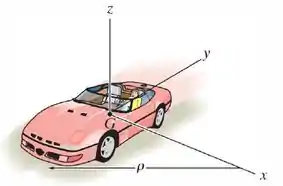
Passo 1

Uma vez que as velocidades angulares são iguais a

ω x = 0

ω y = 0

ω z = V G ρ

E a acelerações angulares

ω ˙ x = ω ˙ y = ω ˙ z = 0

Passo 2

Aplicando a equação do movimento em relação ao eixo x , temos

∑ M x = I x x ω ˙ x - I y y - I z z ω y ω z - I x y ω ˙ y - ω z ω x - I y z ω y 2 - ω z 2 - I z x ( ω ˙ z + ω x ω y )

∑ M x = I x x ( 0 ) - I y y - I z z ( 0 ) v G ρ - I x y 0 - v G ρ 0 - I y z 0 2 - v G ρ 2 - I z x ( 0 + ( 0 ) ( 0 ) )

∑ M x = I y z ρ 2 v G 2

Para direção y , temos

∑ M y = I y y ω ˙ y - I z z - I x x ω z ω x - I y z ω ˙ z - ω x ω y - I z x ω z 2 - ω x 2 - I x y ( ω ˙ x + ω y ω z )

∑ M y = I y y ( 0 ) - I z z - I x x v G ρ ( 0 ) - I y z 0 - ( 0 ) 0 - I z x v G ρ 2 - 0 2 - I x y 0 + ( 0 ) v G ρ

∑ M y = - I z x ρ 2 v G 2

E para a direção z

∑ M z = I z z ω ˙ z - I x x - I y y ω x ω y - I z x ω ˙ x - ω y ω z - I x y ω x 2 - ω y 2 - I y z ( ω ˙ y + ω z ω x )

∑ M z = I z z ( 0 ) - I x x - I y y ( 0 ) 0 - I z x 0 - ( 0 ) v G ρ - I x y 0 2 - 0 2 - I y z ( 0 + v G ρ ( 0 ) )

∑ M z = 0

Resposta

Portanto a equação do movimento rotacional em torno de x ,   y ,   z são ∑ M x = I y z ρ 2 v G 2 , ∑ M y = - I z x ρ 2 v G 2 e ∑ M z = 0 .

Ver Outros Exercícios desse livro