Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 115

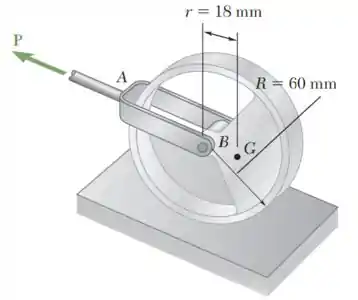
O centro de gravidade G de uma roda desbalanceada de 1,5 kg está localizado a uma distância r = 18 mm de seu centro geométrico B. O raio da roda é R = 60 mm e seu raio de giração em relação ao centro de massa é 44 mm. No instante mostrado na figura, o centro B da roda tem uma velocidade de 0,35 m/s e uma aceleração de 1,2 m/s2 , ambas dirigidas para a esquerda. Sabendo que a roda rola sem deslizar e desprezando a massa do braço AB, determine a força horizontal P aplicada a esse braço.

Passo 1

O exercício pede que a gente determine a força horizontal P aplicada a esse braço.

Cinemática: Escolha VB positivo e aB para esquerda.

Trans. com B + Rotação sobre B = Movimento de rotação

a ¯ = a k + r ω 2 + + r R a B ↑

Cinética:

+ ) Σ M C = Σ M C c f f : P R - W r = m a - y r + m a - x R + I - α P R - m g r = m r R a B r + m a B + r ω 2 R + m k - 2 a B R = m a B r 2 R + R + k - 2 R + m r v B r 2 R P = m g r R + m a B 1 + r 2 + k 2 R 2 + m r R 2 v B 2

(1)

Passo 2

Substituindo:

m = 1.5 k g r = 0.018 m R = 0.06 m k - = 0.044 m m   e   g = 9.81 m / s 2   n a   E q . ( 1 )   P = 1.5 ( 9.81 ) 0.018 0.06 + 1.5 a B 1 + 0.018 2 + 0.044 2 0.06 2 + 1.5 0.018 0.06 2 v B 2 P = 4.4145 + 2.4417 a 13 + 7.5 v b 2

(2)

v B = 0.35 m / s ← ;               v B = + 0.35 m / s a B = 1.2 m / s 2 ← ;                 a B = + 1.2 m / s 2

Passo 3

Substituindo na Eq.(2):

P = 4.4145 + 2.4417 ( + 1.2 ) + 7.5 ( + 0.35 ) 2 = 4.4145 + 2.9300 + 0.9188 = + 8.263 N

Resposta

P = 8.26 N ←

Ver Outros Exercícios desse livro