Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 24

As componentes da deformação em um ponto são ε x = - 480 ( 10 - 6 ) , ε y = 650 ( 10 - 6 ) , γ x y = 780 ( 10 - 6 ) e ε z = 0 . Determine (a) as deformações principais, (b) a deformação por cisalhamento máxima no plano x-y e (c) a deformação por cisalhamento máxima absoluta.

Passo 1

Começaremos o exercício calculando o centro e o raio do círculo de Mohr:

ε C = ε x + ε y 2 = - 480 10 - 6 + 650 ( 10 - 6 ) 2 → ε C = 85 10 - 6

R = ε y - ε C 2 + γ x y 2 2 = 650 10 - 6 - ( 85 ) ( 10 - 6 ) 2 + 780 ( 10 - 6 ) 2 2

R = 686,53 ( 10 - 6 )

Passo 2

Agora iremos esboçar o círculo de Mohr para o sistema em estudo, com as coordenadas A ( ε x ; 0,5 γ x y ) e C ( ε C ; 0 ) :

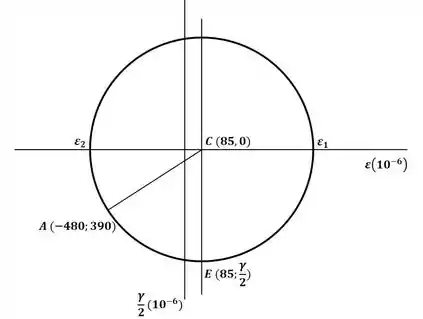
Do círculo de Mohr, podemos obter o valor das deformações principais no plano representadas pelas coordenadas dos pontos ε 1 e ε 2 :

ε 1 = ε C + R = 85 10 - 6 + 686,53 10 - 6 → ε 1 = 771,53 ( 10 - 6 )

ε 2 = ε C - R = 85 10 - 6 - 686,53 10 - 6 → ε 2 = - 601,53 ( 10 - 6 )

Agora iremos encontrar a deformação máxima por cisalhamento máxima no plano x-y, representado pelo ponto E no círculo de Mohr:

γ m a x = 2 R = 2 ( 686,53 ) ( 10 - 6 )

γ m a x = 1373,1 ( 10 - 6 )

Passo 3

E, por fim, iremos encontrar o cisalhamento máximo através da construção dos três círculos da figura a seguir:

ε m a x = ε 1

ε i n t = 0

ε m i n = ε 2  

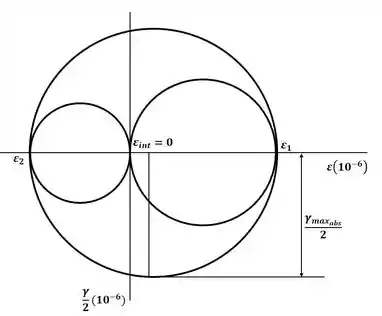
Sendo assim, dos três círculos de Mohr, a deformação por cisalhamento máxima absoluta é dada por:

γ a b s m a x = ε m a x - ε m i n = 773,21 10 - 6 - ( - 601,53 ) ( 10 - 6 )

γ a b s m a x = 1374,7 ( 10 - 6 )

Resposta

ε 1 = 771,53 ( 10 - 6 )

ε 2 = - 601,53 ( 10 - 6 )

γ m a x = 1373,1 ( 10 - 6 )

γ a b s m a x = 1374,7 ( 10 - 6 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O estado plano de tensão indicado é o que se espera que ocorra com uma peça fundida de alumínio. Sabendo que para a liga de alumínio utilizada σ L T = 80M P a e σ L C = 200M P a e usando o critério de
Espera-se que o estado plano de tensão mostrado ocorra em uma base fundida de alumínio. Sabendo que para a liga de alumínio utilizada ocorrer σ L T = 10k s i e σ L C = 30k s i e usando o critério de M
O estado plano de tensão indicado é o que se espera que ocorra com uma peça fundida de alumínio. Sabendo que para a liga de alumínio utilizada σ L T = 80M P a e σ L C = 200M P a e usando o critério de
Resolva o Problema 7.87 usando o critério da energia de distorção máxima.
Espera-se que o estado plano de tensão mostrado ocorra em uma base fundida de alumínio. Sabendo que para a liga de alumínio utilizada ocorrer σ L T = 10k s i e σ L C = 30k s i e usando o critério de M