Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 64
A viga está sujeita a uma força de cisalhamento Determine o fluxo de cisalhamento nos pontos A e B
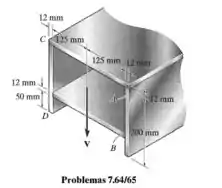
Passo 1
Dados da questão:
A questão pede o fluxo de cisalhamento em A e B:
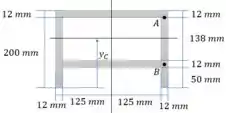
Estratégia de resolução: Começamos encontrado o centroide e calculando o momento de inércia. Depois calculamos os momentos estáticos nos pontos de interesse e aplicamos a equação de fluxo de cisalhamento.
Passo 2
Vamos calcular o centroide.
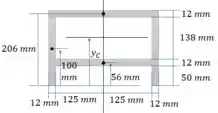
Passo 3
Agora podemos calcular o momento de inércia
Passo 4
Agora vamos calcular o momento estático. A figura destaca em laranja o momento estático de e em amarelo de .
Passo 5
Agora aplicamos a equação de fluxo de cisalhamento
Resposta
Exercícios de Livros Relacionados
A viga em balanço A B consiste de metade de um tubo de parede fina, com raio médio de 30m m e espessura da parede de 9,5m m . Sabendo-se que a carga vertical P passa através do centroide C da seção tr
Dois perfis laminados de aço W 130 × 23.8 podem ser soldados em A e B , de qualquer uma das três maneiras mostradas, para formar uma viga composta. Sabendo-se que para cada uma das soldas a força cisa
Uma placa de 4 mm de espessura é encurvada como mostrado e depois usada como uma viga. Para uma força cortante vertical de 12 kN, determinar (a) a tensão de cisalhamento no ponto A; (b) a máxima tensã
Determinar a tensão cisalhamento no ponto A de um tubo na parede fina como a seção transversal mostrada, casada por uma força cortante vertical V.
O projeto de uma viga requer a soldagem de quatro placas horizontais à uma placa vertical de 12,7x127 mm como mostrado. Para uma força cortante vertical V determinar a dimensão h para que o fluxo de c