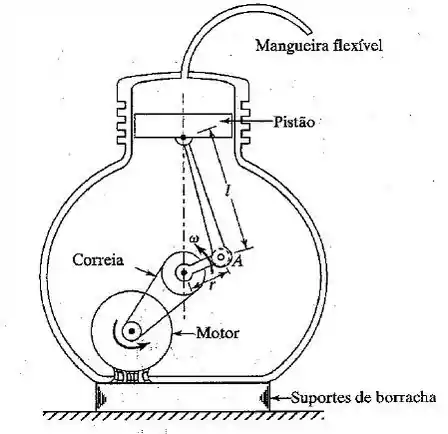
Um compressor de ar de um cilindro com de massa está montado sobre suportes de borracha, como mostra a Figura 3.54. As constantes de rigidez e amortecimento dos suportes de borracha são dadas por e , respectivamente. Se o desequilibrio do compressor for equivalente à massa de localizada na extremidade da manivela (ponto ), determine a resposta do compressor à velocidade da manivela de . Suponha que e
Passo 1
Equação do movimento
Em que
Resposta de estado estacionário
Em que
Em que