Constata-se que uma viga uniforme simplesmente apoiada em arnbas as extremidades vibra em seu primeiro modo com uma amplitude de 10 mm em seu centre. Se , , , e , determine o máximo momento fletor na viga.
Passo 1
E aí, galerinha!
Vamos ver as possíveis equações da viga pra ver qual a gente vai usar!
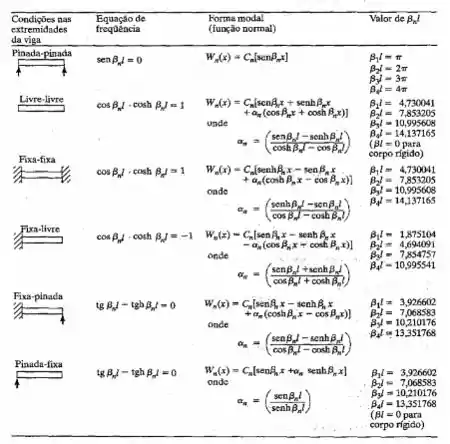
Passo 2
Temos também a seguinte equação...
Uma vez que seno dividido pelo cosseno é a tangente...
Baseado na equação de frequência...
Sendo que...
Se as raízes da equação de frequência são dadas por...
Então, baseando na equação para ...
Como sabemos que , então...
Ficamos então, com...
Derivando ...
Multiplicando e por e integrando de até :
Obtemos que...
E ficamos então, com a seguinte equação...
Substituindo, obtemos que...