6. Constatou-se que a amplitude e o ângulo de fase devido ao desbalanceamento original de um disco de esmeril que funciona a sao e em sentido anti-horário em relação a marca de fase. Quando um peso de teste é acrescentado a em sentido horário em relação a marca de fase e a uma distância radial de em relação ao centro de rotação, observa-se que a amplitude e o ângulo de fase são e em sentido anti-horário. Detemrine a magnitude e a posição angular do peso de balanceamento se ele tiver de ser localizado a de distância radial em relagao ao centro de rotação.
Passo 1
E aí, galerinha!
Simbora lá, meus queridos!
Bom! Vamos dar nomes aos bois... Temos a seguinte configuração para o nosso sistema...
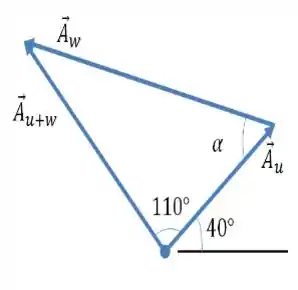
Onde...
Aplicando a lei dos cossenos, podemos obter :
Como :
Passo 2
Dessa forma, para encontrar a massa de balanceamento () requerida que precisa ser colocada, basta usar a fórmula abaixo...
E pra achar a posição angular do peso de balanceamento, no caso , vamos novamente recorrer à lei dos cossenos. Baseado na nossa figura do :
Isolando , temos que...
Como o nosso peso de teste é acrescentado a em sentido horário em relação a marca de fase, então a orientação do nosso ângulo será de...
Pronto! Finalizamos aqui!