Construa o diagrama de Nyquist para um sistema com um grau de liberdade e amortecimento por histerese.
Passo 1
Falaaa galerinha, bora lá??
Conforme mostrado a seguir iremos construir um diagrama de Nyquist para um único grau de liberdade.
Iremos escrever agora as partes reais e imaginárias da equação (1)
Iremos adicionar as duas partes da seguinte maneira:
Passo 2
A expressão (2) pode ser escrita da seguinte maneira
Portanto, a equação (3) mostra que o lugar geométrico de e aumenta de zero e faz parte de um círculo, com centro
E o raio é de
Passo 3
Iremos desenhar o diagrama de Nyquist para um único grau de liberdade, conforme mostrado abaixo.
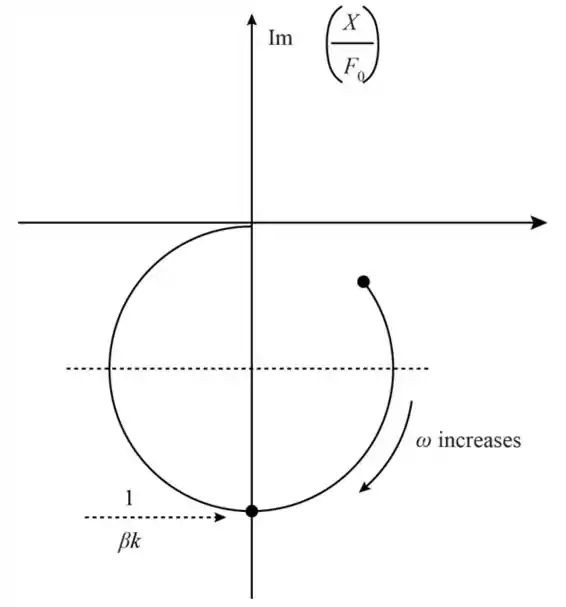
Resposta
Vide a explicação.