Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 8.Problemas - Ex. 12

Uma corda de comprimento l vibra em um meio viscoso. Deduza a equação de movimento considerando a força de amortecimento viscoso.

Passo 1

E aí, galerinha!

Bom! Bora lá!

Vamos começar fazendo um esboço do nosso problema!

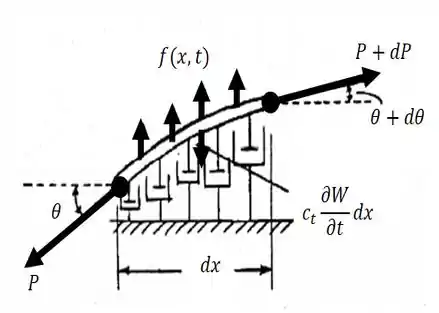
c t no caso aí, é o coeficiente de viscosidade!

Passo 2

Pois muito bem! Aplicando o somatório das forças na direção y , na vertical, temos que...

∑ F y = 0

P + d P sen ⁡ ( θ + d θ ) + f x , t d x - c t ∂ W ∂ t d x - P sen ⁡ θ = ρ d x ∂ 2 W ∂ t 2

Passo 3

Agora, uma vez que podemos escrever...

d P = ∂ P ∂ x d x

sen ⁡ ( θ + d θ ) ≈ ∂ W ∂ x + ∂ 2 W ∂ x 2 d x

Então, a equação das forças do final do P a s s o   2 vai ficar assim...

P + ∂ P ∂ x d x ∂ W ∂ x + ∂ 2 W ∂ x 2 d x + f x , t d x - c t ∂ W ∂ t d x - P sen ⁡ θ = ρ d x ∂ 2 W ∂ t 2

∂ ∂ x P ∂ W ( x , t ) ∂ x + f x , t d x = ρ ∂ 2 W ( x , t ) ∂ t 2 + c t ∂ W ( x , t ) ∂ t d x

Resposta

∂ ∂ x P ∂ W ( x , t ) ∂ x + f x , t d x = ρ ∂ 2 W ( x , t ) ∂ t 2 + c t ∂ W ( x , t ) ∂ t d x

Ver Outros Exercícios desse livro