Enunciado
Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 11.Problemas - Ex. 25
Deduza as equações de diferenças finitas para a vibração forçada de um eixo uniforme fixo-fixo sob torção, usando um total de n pontos de malha.
Passo 1
Faaaalaa galerinha, tudo na boaa?
Vamos resolver mais um exercício???
Então encoxxta!!
A equação de movimento do eixo de vibração forçada pode ser descrita da seguinte maneira
Como é o momento de inércia da massa polar e é a constante de torção da mola.
A equação (1) pode ser reescrita como :
Com isso, as equações acima podem ser reescritas como,
Divida o comprimento do eixo em n-1 parte igual e denote os pontos da malha 1, 2, 3, ...., n, como mostrado na figura a seguir. Cada parte tem comprimento de
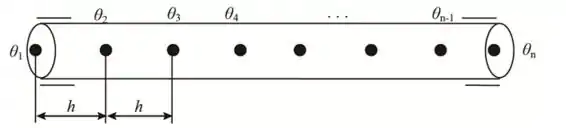
Passo 2
A segunda derivada pode ser substituída pela equação de
Ao combinarmos as equações (2) e (3), a equação de movimento pode ser expressa como:
E denotar a variável de e as variável de e , a equação acima é expressa por
Aplicando a equação em cada ponto da malha
Podemos expressar como matriz:
Passo 3
Condição de contorno
Fim fixo fim fixo. O deslocamento angular é zero em ambas as extremidades fixas
Portanto, a equação da matriz pode ser reescrita como:
Obtendo a equação final como
Com esta matriz surgiu
O problema de autovalores da equação (4) pode ser resolvido facilmente, uma vez que a matriz [A] é uma matriz tri diagonal, portanto comprovado.
Resposta
Vide o passo a passo.