Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 24

Deduza as equações de movimento do sistema mostrado na Figura 6.29.

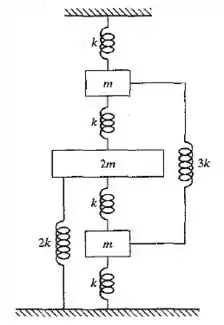
Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto, que dessa vez é bem curtinha!

Inicialmente vamos definir as massas do topo, do meio e debaixo como x 1 , x 2 , x 3 , respectivamente.

Assim, nós teremos as seguintes equações do movimento:

m →   x 1 ¨ = - k   x 1 - k x 1 - x 2 - 3 k ( x 1 - x 3 )

2 m →   x 2 ¨ = - 2   k   x 2 - k x 2 - x 1 - k x 2 - x 3

m →   x 3 ¨ = - k   x 3 - 3 k x 3 - x 1 - k ( x 3 - x 2 )

Agora, ficou fácil para montarmos o cálculo das matrizes, teremos que:

m           0           0 0         2 m           0 0           0             m x 1 ¨ x 2 ¨   x 3 ¨ + 5 k         - k         - 3 k - k             4 k         - k - 3 k         - k             5 k x 1 x 2   x 3 = 0 0   0

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro