Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 29

Deduza a matriz de massa de cada um dos sistemas mostrados nas figuras 6.17 a 6.21 utilizando as coordenadas indicadas.

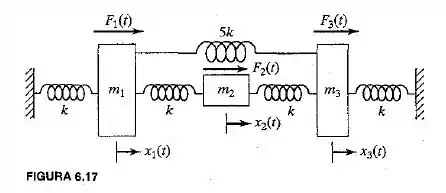
Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

Inicialmente, se localizem na figura 6.19, a terceira a ser considerada.

Nós usaremos a expressão da energia cinética para derivar a matriz de massa, novamente. Vamos dizer que as coordenadas generalizadas são   x 1 ,   x 2 ,   x 3 . A energia cinética do sistema se dá por:

T = 1 2   J G   θ ˙ + 1 2 2 m x G 2 ˙ + 1 2 ( 5 m ) x 2 2 ˙

Onde:

J G = 1 12 2 m 5 l 2 = 25 6 m l 2

x G = x 1 + x 3 2

θ = x 1 - x 3 5 l

Dessa forma a energia cinética do sistema pode ser reescrita como:

T = 1 2 25 6 m l 2 x 1 - x 3 ˙ ˙ 5 l 2 + 1 2 2 m x 1 + x 3 ˙ ˙ 2 2 + 1 2 ( 5 m ) x 2 2 ˙

Isso pode ser escrito em matriz como:

T = 1 2 ( x 1 ˙   x 2 ˙   x 3 ˙ ) m     x 1 ˙ x 2 x 3 ˙ ˙

Dessa forma, a matriz de massa é dada por:

m = 2 3 m l 2             0               1 3 0                           5                     0 1 3                         0                   2 3

Resposta

m = 2 3 m l 2             0               1 3 0                           5                     0 1 3                         0                   2 3

Ver Outros Exercícios desse livro