Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 3.Problemas - Ex. 63

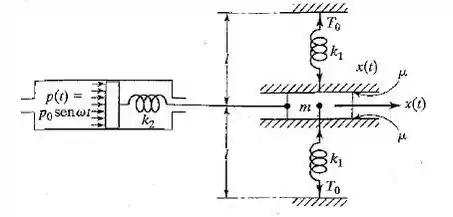
Derive a equação de movimento da massa m mostrada na Figura 3.59 quando a variação da pressão no cilindro for senoidal. As duas molas com rigidez k 1 estão inicialmente sob uma tensão T 0 , e o coeficiente de atrito entre a massa e as superfícies de contato e μ .

Passo 1

Seja x (t) = deslocamento da massa m

Novo comprimento de cada mola: , k 1 = l 2 + x 2 1 / 2

Nova tensão em cada mola k 1 = T = l 2 + x 2 - l k 1 + T 0

Componente horizontal da nova tensão em cada mola k 1   = T = l 2 + x 2

Componente vertical da nova tensão em cada mola   k 1 = T l l 2 + x 2

Fricção total da força   μ m g + 2 T l l 2 + x 2

Passo 2

Quando a massa se move para a direita

Equação do movimento de massa m

m x ¨ + k 2 x + 2 T x l 2 + x 2 - μ m g + 2 T l l 2 + x 2 = P 0 A s i n ⁡ ω t

Em que A = área do pistão

i.e.,  m x ¨ + x k 2 + 2 T 0 l = μ m g + 2 μ T 0 + p 0 A s i n ⁡ ω t

Passo 3

Similarmente, quando a massa se move para a esquerda

m x ¨ + x k 2 + 2 T 0 l = - μ m g - 2 μ T 0 + P 0 A s i n ⁡ ω t

Resposta

μ m g + 2 μ T 0 + p 0 A s i n ⁡ ω t

- μ m g - 2 μ T 0 + P 0 A s i n ⁡ ω t

Ver Outros Exercícios desse livro