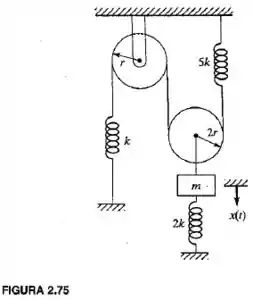
Derive a equação de movimento com a utilização do princípio de conservação da energia para cada um dos sistemas mostrados nas figuras 2.74 e 2.75.
Fonte: Rao Vibrações Mecânicas – 4ª ed
Passo 1
Fala aí!
Vamos para mais uma!
Já resolvemos esse problema pelo método da segunda lei de Newton, agora o problema quer que resolvamos através do método da conservação da energia.
Bora lembrar que a conservação da energia analisa dois instantes distintos, e que a energia mecânica no instante 1 deve ser igual a energia mecânica no instante 2.
Vamos lá!
Passo 2
Dito isso, temos que a energia cinética do sistema é a energia cinética da massa somado com o da polia resultante (podemos relembrar na resolução do problema 2.47):
E a energia potencial do sistema é:
Onde ,
Passo 3
Assim:
Resposta
Portanto: