Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 1.Problemas - Ex. 57

Determine as amplitudes máxima e mínima do movimento combinado x t = x 1 t + x 2 ( t ) quando x 1 t = 3 sin ⁡ 30 t   e   x 2 t = 3 sin ⁡ 29 t . Determine também a frequência de batimentos correspondente a x ( t ) .

Passo 1

Falaaa meus queridos, vamo pra mais uma questãozinha!

Escrevendo a equação dos dois movimentos, temos que:

x t = 3 sin ⁡ 30 t + 3 sin ⁡ 29 t

Por definição da trigonometria, sabemos que:

sin ⁡ A + sin ⁡ B = 2 sin ⁡ A + B 2 cos ⁡ A - B 2

Dito isso, conseguimos escrever a equação dos dois movimentos da seguinte forma:

x t = ( 6 cos ⁡ t 2 ) sin ⁡ 59 2 t

Passo 2

Tendo posse dessa equação, conseguimos desenvolver o seguinte gráfico:

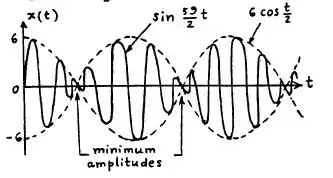
Por observação da equação e gráfico, podemos concluir que a amplitude vale 6 cos ⁡ t 2 , e varia ao longo do tempo com um valor máximo de 6 e um valor mínimo de 0 . A frequência dessa oscilação equivale a ω b = 1 .

Observação: A frequência da oscilação vale o dobro da frequência do termo 6 cos ⁡ t 2 já que dois picos passam em cada ciclo de ( 6 cos ⁡ t 2 ) .

Resposta

A amplitude vale 6 cos ⁡ t 2 , e varia ao longo do tempo com um valor máximo de 6 e um valor mínimo de 0 . A frequência dessa oscilação equivale a ω b = 1 .

Ver Outros Exercícios desse livro