Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 1.Problemas - Ex. 7

Determine a constante elástica equivalente do sistema mostrado na Figura 1.59.

Passo 1

Saalve galerinha, tudo certo?! Então, nessa questão ele nos pede a constante elástica equivalente pra o sistema apresentado na figura abaixo:

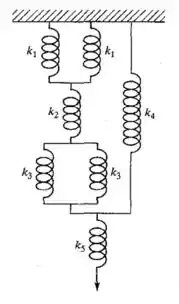
Então, nessa figura a gente tem 5 constantes diferentes e pra a gente conseguir fazer o sistema, a gente tem que dividir em partes. Belezinha? Bora lá!

Passo 2

Aqui a gente começa com k 1 , k 2 e k 3 . Temos que:

1 k e q 1 = 1 2 k 1 + 1 k 2 + 1 2 k 3

A partir disso temos que:

k e q 1 = 2 k 1 k 2 k 3 k 2 k 3 + 2 k 1 k 3 + k 1 k 2

E agora a gente tem isso:

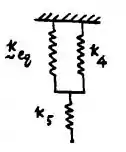
Passo 3

E falta pra gente incluir nesse negócio todo o k 4 e k 5 pra termos o k e q t o t a l . Pra isso fica fácil porque a gente já tem o k e q 1 . Logo:

1 k e q t o t a l = 1 k e q 1 + k 4 + 1 k 5

Portanto:

k e q t o t a l = k 5 ( k e q 1 + k 4 ) k 5 + k 4 + k e q 1

Agora vem a parte mais legal: JUNTAR TUDO! Aplicando o valor de k e q 1 na equação, temos que:

k e q t o t a l = k 2 k 3 k 4 k 5 + 2 k 1 k 3 k 4 k 5 + k 1 k 2 k 4 k 5 + 2 k 1 k 2 k 3 k 5 k 2 k 3 k 4 + k 2 k 3 k 5 + 2 k 1 k 3 k 4 + 2 k 1 k 3 k 5 + k 1 k 2 k 4 + k 1 k 2 k 5 + 2 k 1 k 2 k 3

Resposta

k e q t o t a l = k 2 k 3 k 4 k 5 + 2 k 1 k 3 k 4 k 5 + k 1 k 2 k 4 k 5 + 2 k 1 k 2 k 3 k 5 k 2 k 3 k 4 + k 2 k 3 k 5 + 2 k 1 k 3 k 4 + 2 k 1 k 3 k 5 + k 1 k 2 k 4 + k 1 k 2 k 5 + 2 k 1 k 2 k 3

Ver Outros Exercícios desse livro