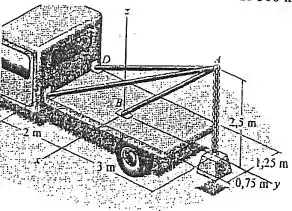
Determine a força que atua ao longo do eixo de cada um dos três suportes para sustentar o bloco de 500 kg.
Passo 1
Fala! Queremos a intensidade das forças nos cabos.
Para encontrar o valor da força em cada cabo, o que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas.
Logo, fazendo o diagrama de corpo livre tem-se:
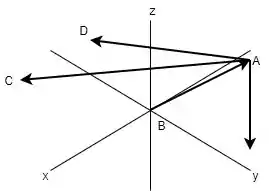
Em seguida, o equilíbrio de forças deve ser analisado nas três dimensões x, y e z, pelo fato de as forças estarem atuando em todos esses três sentidos.
Como a geometria do problema é mais complexa, é mais jogo a gente escrever as forças na forma vetorial. Fazer a soma vetorial, e igualar cada componente dessa soma a zero, já que estamos no equilíbrio, bele? Vamos!
Passo 2
Tem-se que o bloco exerce uma força peso para baixo que tem intensidade de . Então escrevendo vetorialmente temos:
Também é possível denotar as forças , e na forma vetorial. O que a gente precisa fazer é achar um vetor unitário na direção e sentido da força, e multiplicar a intensidade da nossa força por ele.
Percebe que para a AB, um vetor no sentido da força seria o que sai de B e vai para A. Podemos acha-lo pela diferença entre essas coordenadas desses pontos. Fazendo final menos inicial:
Aí para achar o vetor unitário só dividir esse cara pelo módulo dele. Nossa força em forma vetorial fica:
Fazemos o mesmo para as outras forças. Aqui nosso vetor sai de A e vai para C:
Prontinho!
Passo 3
O equilíbrio requer quer o somatório de forças em cada dimensão seja nulo, ou seja:
Olhando para cada eixo, vamos igualar a soma em cada componente a zero.
Por fim para a componente :
Passo 4
Agora, como há três equações encontradas, é possível montar um sistema linear de equações e determinar a solução dele, cuja solução será o valor das forças.
Resolvendo este sistema, obtem-se: