Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 49

  1. Determine as frequências naturais do sistema mostrado na Figura 6.26 com m 1 = m 2 =   m 3 = m ,   l 1 =   l 2 =   l 3 = l 4 = l / 4   .

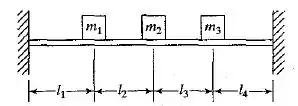
  2. Determine as frequências naturais da viga quando m = 10 k g ,   l = 0,5 m , a seção transversal é uma seção circular sólida com 2,5 cm de diâmetro e o material é aço.
  3. Considere utilizar uma seção transversal circular oca, retangular sólida ou retangular oca para a viga, de modo a obter as mesmas frequências naturais como em (b). Identifique a seção transversal correspondente ao peso mínimo da viga.

Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

  1. Bom, para esse enunciado, o problema anterior, 6.21, já nos fornece um sistema de equações para flexibilidade e massa, que com as devidas substituições vão ficar:

    2. a = l 3 64 E I 9 / 64         1 / 6         13 / 192 1 / 6                 1 / 3                       1 / 6 13 / 192         1 / 6           9 / 64

    m = m 1       0         0 0         1         0 0         0           1 ;

    Dito isso, o produto dessas matrizes será o seguinte:

    D = a m = m l 3 E I 0,0021775         0,0026042         0,0010579 0,0026042           0,0052083             0,0026042 0,0010579         0,0026042           0,0021973

    Esse sistema nos dá a seguinte equação de frequência:

    0,0021775 - α         0,0026042         0,0010579 0,0026042           0,0052083 - α             0,0026042 0,0010579         0,0026042           0,0021973 - α = 0

    Ou seja, tirando da forma matricial:

    0,0021973 - α   0,0052083 - α 0,0021973 - α - 0,0026042 2 - 0,0026042 0,0026042 0,0021973 - α - 0,0010579 0,0026042 + 0,0010579 0,0026042 2 - 0,0010579   0,0052083 - α = 0

    Ou seja:

    α 3 - 0,96029 ∙ 10 - 2 α 2 + 0,1303355 ∙ 10 - 4 α - 0,0038623 ∙ 10 - 6 = 0

    As raízes desta mega expressão vão ser:

    α 1 = 0,000421453 → ω 1 = 48,71082 k / m

    α 2 = 0,00113955 → ω 2 = 29,62329 k / m

    α 3 = 0,00804192 → ω 3 = 11,15116 k / m

    Passo 2

    Agora, vamos para o item b, pessoal.

  2. Iniciamos analisando os dados propostos e definindo E = 2,07 ∙ 10 11 N / m 2 , sabendo que o material é aço.

    3. Como temos uma seção circular, fazemos o cálculo da inércia para a mesma:

    I = π 64 d 4 = 1,9175 ∙ 10 - 8 m 4

    E I m l 3 = 56,3505 = k m

    De posse desses dados, usamos o esquema do item anterior para encontramos as raízes de fato. E teremos:

    ω 1 = 48,71082 56,3505 = 2744,8791   r a d / s

    ω 2 = 29,62329 56,3505 = 1669,2872   r a d / s

    ω 3 = 11,15116 56,3505 = 628,3734   r a d / s

    Passo 3

  3. Para obtermos outros sistemas com a mesma frequência natural, significa que precisamos ter o mesmo valor de inércia. Vamos então, por partes do que foi pedido:
  1. Seção circular sólida com d = 2,5   c m .

    2. Pra esse, nós já calculamos.

    I = 1,9175 ∙ 10 - 8 m 4

    A = π 4 d 2 = 4,90875 c m 2

  2. Seção circular oca.

    3. Nesse, vamos fazer que d 0 = 5 t , sendo d 0 o diâmetro total, e t o diâmetro externo. Teremos que:

    I = π 64 d 0 4 - d i 4 = π 64 625 - 81 t 2 = 26,7036 t 4

    Agora é só igualar com o I que já temos. Iremos encontrar:

    t = 0,5177   c m ,   d 0 = 2,5885 c m ,   d i = 1,5531   c m

    A = π 4 d 0 2 - d i 2 = 3,3680 c m 2

  3. Seção retangular sólida.

    4. Vamos fazer que b = 2 a , sendo “ a ” a base e “ b ” a altura.

    I = 1 12 a b 3 = 2 3 a 4

    Igualando com nosso I, teremos:

    a = 1,3023   c m ,   b = 2,6046   c m

    A = a b = 3,3920   c m 2

  4. Seção retangular oca.

Para fazer essa, vamos seguir os parâmetros da seguinte ilustração:

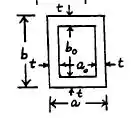
Vamos fazer que b = 5 t ,   b 0 = 3 t ,   a = 2,5 t ,   a 0 = 0,5 t .

I = 1 12 a b 3 - a 0 b 0 3 = 1 12 2,5 ∙ 125 ∙ t 4 - 0,5 ∙ 27 ∙ t 4 = 24,9167   t 4

Igualando com nosso I:

t = 0,5267   c m ,   a = 1,3167   c m ,   b = 2,6335   c m ,   a 0 = 0,2634   c m ,

  b 0 = 1,5801   c m

A = a b - a 0 b 0 = 3,0512   c m 2

Resposta

  1. α 1 = 0,000421453 → ω 1 = 48,71082 k / m

    α 2 = 0,00113955 → ω 2 = 29,62329 k / m

    α 3 = 0,00804192 → ω 3 = 11,15116 k / m

  2. ω 1 = 2744,8791   r a d / s

    ω 2 = 1669,2872   r a d / s

    ω 3 = 628,3734   r a d / s

  3. Concluímos que a seção retangular oca tem a menor área e o menor peso de todas consideradas.
Ver Outros Exercícios desse livro